2.1 - Multiclass classification - Inside Deep Learning

We are going to add a crucial element: the activation function. This function will allow us to modify the output to suit our problem, in this case the classification of multiple classes.

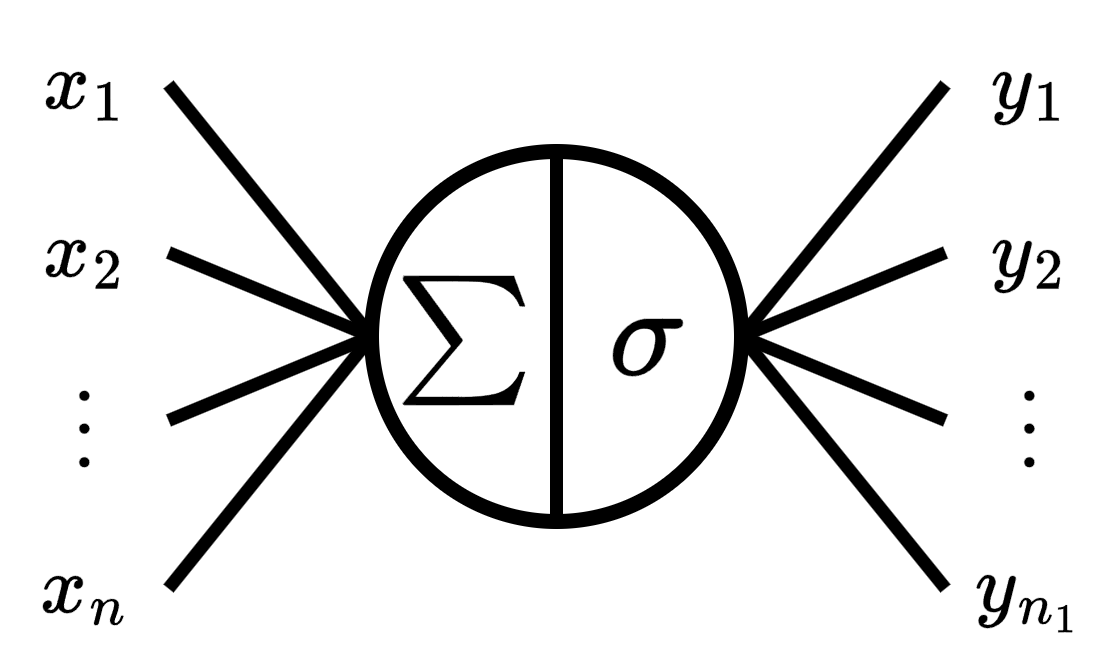
The softmax function will allow us to convert an input into the probability of remaining in the classes.

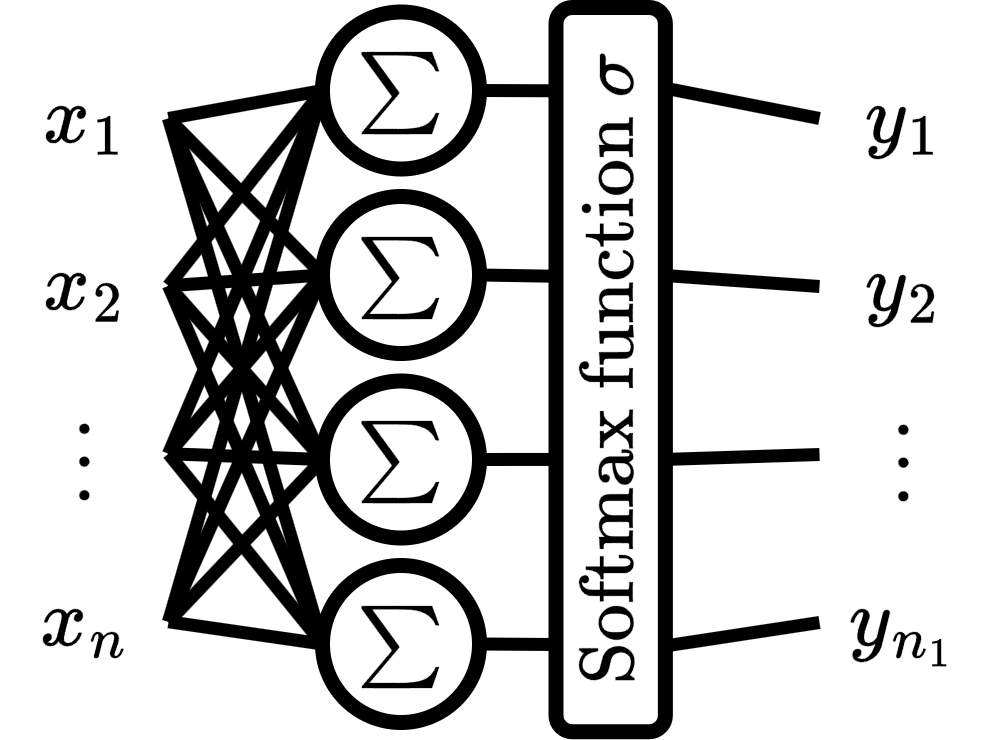
We can interpret the perceptron with softmax as a dense layer and an activation layer, this interpretation will be useful later in chapter 3.

Purpose of this Notebook:

The purposes of this notebook are:

Create a dataset for classification regression task
Create our own Perceptron class from scratch
Add Softmax function as activation function from scratch
Calculate the gradient descent from scratch
Train our Perceptron
Compare our Perceptron to the one prebuilt by PyTorch
[Extra] Calculate the gradient descent by another way

import torch
from torch import nn

from platform import python_version
python_version(), torch.__version__

('3.12.12', '2.9.0+cu128')

device = 'cpu'
if torch.cuda.is_available():
    device = 'cuda'
device

'cpu'

torch.set_default_dtype(torch.float64)

def add_to_class(Class):  
    """Register functions as methods in created class."""
    def wrapper(obj):
        setattr(Class, obj.__name__, obj)
    return wrapper

Dataset¶

create dataset¶

\begin{align*} \mathbf{X} &\in \mathbb{R}^{m \times n} \\ \mathbf{Y} &\in \mathbb{R}^{m \times n_{1}} \end{align*}

(1)

where $n_{1}$ is the number of classes.

from sklearn.datasets import make_classification

M: int = 10_100 # number of samples
N: int = 5 # number of input features
CLASSES: int = 3 # number of classes

X, Y = make_classification(
    n_samples=M, 
    n_features=N, 
    n_classes=CLASSES, 
    n_informative=N - 1, 
    n_redundant=0
)

print(X.shape)
print(Y.shape)

(10100, 5)
(10100,)

one hot encoding¶

Y_hat = nn.functional.one_hot(
    torch.tensor(Y, device=device).long(), 
    CLASSES
).type(torch.float32)
Y_hat.shape

torch.Size([10100, 3])

split dataset into train and valid¶

X_train = torch.tensor(X[:100], device=device)
X_valid = torch.tensor(X[100:], device=device)
X_train.shape, X_valid.shape

(torch.Size([100, 5]), torch.Size([10000, 5]))

Y_train, Y_valid = Y_hat[:100], Y_hat[100:]
Y_train.shape, Y_valid.shape

(torch.Size([100, 3]), torch.Size([10000, 3]))

delete raw dataset¶

del X
del Y
del Y_hat

Model¶

weights and bias¶

\begin{align*} \mathbf{W} &\in \mathbb{R}^{n \times n_{1}} \\ \mathbf{b} &\in \mathbb{R}^{n_{1}} \end{align*}

(2)

class SoftmaxClassifier:
    def __init__(self, n_features: int, n_classes: int):
        self.w = torch.randn(n_features, n_classes, device=device)
        self.b = torch.randn(n_classes, device=device)

    def copy_params(self, torch_layer: nn.modules.linear.Linear):
        """
        Copy the parameters from a module.linear to this model.

        Args:
            torch_layer: Pytorch module from which to copy the parameters.
        """
        self.b.copy_(torch_layer.bias.detach().clone())
        self.w.copy_(torch_layer.weight.T.detach().clone())

weighted sum and softmax function¶

weighted sum

\mathbf{Z}(\mathbf{X}) = \mathbf{X} \mathbf{W} + \mathbf{b} \\ \mathbf{Z} : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n_{1}}

(3)

softmax function

\sigma(\mathbf{z}_{i,:})_{j} = \frac{\exp(z_{ij})} {\sum_{k=1}^{n_{1}}(\exp(z_{ik}))} \in \mathbb{R}^{+}

(4)

then

\sigma(\mathbf{z}_{i,:}) = \begin{bmatrix} \sigma(\mathbf{z}_{i,:})_{1} & \sigma(\mathbf{z}_{i,:})_{2} & \cdots & \sigma(\mathbf{z}_{i,:})_{n_{1}} \end{bmatrix}

(5)

therefore

\mathbf{\Sigma(Z)} = \begin{bmatrix} \sigma(\mathbf{z}_{1,:}) \\ \sigma(\mathbf{z}_{2,:}) \\ \vdots \\ \sigma(\mathbf{z}_{m,:}) \end{bmatrix} \\ \mathbf{\Sigma} : \mathbb{R}^{m \times n_{1}} \rightarrow \mathbb{R}^{m \times n_{1}}

(6)

@add_to_class(SoftmaxClassifier)
def predict(self, x: torch.Tensor) -> torch.Tensor:
    """
    Predict the output for input x.

    Args:
        x: Input tensor of shape (n_samples, n_features).

    Returns:
        y_pred: Predicted output tensor of shape (n_samples, n_classes).
    """
    # weighted sum
    z = torch.matmul(x, self.w) + self.b
    # avoid underflow and overflow
    z_norm = z - torch.max(z, dim=1, keepdims=True)[0]
    # softmax function
    z_exp = torch.exp(z_norm)
    return z_exp / z_exp.sum(1, keepdims=True) # y_pred

Cross-entropy loss¶

Cross-entropy loss

L(\mathbf{\hat{Y}}) = - \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n_{1}}( y_{ij} \log_{e}(\hat{y}_{ij}) ) \\ L : \mathbb{R}^{m \times n_{1}} \rightarrow \mathbb{R}

(7)

Remark: for this case $\mathbf{\hat{Y}}$ is $\mathbf{\Sigma(Z)}$ .
It is not mandatory to use softmax for cross-entropy loss, but some modules like PyTorch require softmax to use cross-entropy loss.

Vectorized form

L(\mathbf{\hat{Y}}) = - \frac{1}{m} \sum_{i=1}^{m} \left( \mathbf{y}_{i,:}^\top \log_{e}(\mathbf{\hat{y}}_{i,:}) \right)

(8)

or

L(\mathbf{\hat{Y}}) = - \frac{1}{m} \text{sum} \left( \mathbf{Y} \odot \log_{e}(\mathbf{\hat{Y}}) \right)

(9)

@add_to_class(SoftmaxClassifier)
def cross_entropy_loss(self, y_true: torch.Tensor, y_pred: torch.Tensor) -> float:
    """
    CE loss function between target y_true and y_pred.

    Args:
        y_true: Target tensor of shape (n_samples, n_classes).
        y_pred: Predicted tensor of shape (n_samples, n_classes).

    Returns:
        loss: CE loss between predictions and true values.
    """
    loss = y_true * torch.log(y_pred)
    return - loss.sum().item() / len(y_true)

@add_to_class(SoftmaxClassifier)
def evaluate(self, x: torch.Tensor, y_true: torch.Tensor) -> float:
    """
    Evaluate the model on input x and target y_true using CE.

    Args:
        x: Input tensor of shape (n_samples, n_features).
        y_true: Target tensor of shape (n_samples, n_classes).

    Returns:
        loss: CE loss between predictions and true values.
    """
    y_pred = self.predict(x)
    return self.cross_entropy_loss(y_true, y_pred)

Gradient¶

Cross-entropy derivative¶

\begin{align*} \frac{\partial L}{\partial \hat{y}_{pq}} =& -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial}{\partial \hat{y}_{pq}} \left( y_{ij} \log_{e}(\hat{y}_{ij}) \right) \\ &= -\frac{1}{m} \left(\frac{y_{pq}}{\hat{y}_{pq}} \right) \end{align*}

(10)

for all $p = 1, \ldots, m$ and $q = 1, \ldots, n_{1}$ .

Remark: $\hat{y}_{pq}$ must be different of 0, $\hat{y}_{pq} \neq 0$ . Softmax returns positive real values, $\sigma(z) \in \mathbb{R}^{+}$ .

In general

\frac{\partial L}{\partial \hat{\mathbf{Y}}} = -\frac{1}{m} \left( \mathbf{Y} \oslash \hat{\mathbf{Y}} \right)

(11)

Note: $\oslash$ is element-wise divide.

softmax derivative¶

\begin{align*} \frac{\partial L}{\partial z_{pq}} =& -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial}{\partial z_{pq}} \left( y_{ij} \log_{e}(\hat{y}_{ij}) \right) \\ =& \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial L}{\partial \sigma_{ij}} \frac{\partial \sigma_{ij}}{\partial z_{pq}} \end{align*}

(12)

for all $p = 1, \ldots, m$ and $q = 1, \ldots, n_{1}$ .

where

\frac{\partial \sigma_{ij}}{\partial z_{pq}} = \begin{cases} \sigma(z_{pq})(1 - \sigma(z_{pq})) & \text{if } i=p, j=q \\ -\sigma(z_{pq}) \sigma(z_{ij}) & \text{if } i=p, j \neq q \\ 0 & \text{otherwise} \end{cases}

(13)

therefore

\begin{align*} \frac{\partial L}{\partial z_{pq}} =& \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial L}{\partial \sigma_{ij}} \frac{\partial \sigma_{ij}}{\partial z_{pq}} \\ =& \sum_{j=1}^{n_{1}} \frac{\partial L}{\partial \sigma_{pj}} \begin{cases} \sigma(z_{pq})(1 - \sigma(z_{pq})) & \text{if } j=q \\ -\sigma(z_{pq}) \sigma(z_{pj}) & \text{if } j \neq q \end{cases} \end{align*}

(14)

Check softmax function and its derivative for more information about the softmax derivative.

In general

\frac{\partial L}{\partial \mathbf{Z}} = \mathbf{\Sigma} \odot \left( \frac{\partial L}{\partial \mathbf{\Sigma}} - \left( \frac{\partial L}{\partial \mathbf{\Sigma}} \odot \mathbf{\Sigma} \right) \mathbf{1} \right)

(15)

where $\mathbf{1} \in \mathbb{R}^{n_{1} \times n_{1}}$ .

weighted sum derivative¶

respect to bias¶

\begin{align*} \frac{\partial L}{\partial b_{q}} =& -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial}{\partial b_{q}} \left( y_{ij} \log_{e}(\hat{y}_{ij}) \right) \\ &= \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial L}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial b_{q}} \\ &= \sum_{i=1}^{m} \frac{\partial L}{\partial z_{iq}} \end{align*}

(16)

for all $q = 1, \ldots, n_{1}$ .

In general

\frac{\partial L}{\partial \mathbf{b}} = \mathbf{1} \frac{\partial L}{\partial \mathbf{Z}}

(17)

where $\mathbf{1} \in \mathbb{R}^{m}$ .

respect to weight¶

\begin{align*} \frac{\partial L}{\partial w_{pq}} =& -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial}{\partial w_{pq}} \left( y_{ij} \log_{e}(\hat{y}_{ij}) \right) \\ &= \sum_{i=1}^{m} \sum_{j=1}^{n_{1}} \frac{\partial L}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial w_{pq}} \\ &= \sum_{i=1}^{m} x_{ip} \frac{\partial L}{\partial z_{iq}} \end{align*}

(18)

for all $p = 1, \ldots, m$ and $q = 1, \ldots, n_{1}$ .

In general

\frac{\partial L}{\partial \mathbf{W}} = \mathbf{X}^\top \frac{\partial L}{\partial \mathbf{Z}}

(19)

@add_to_class(SoftmaxClassifier)
def update(self, x: torch.Tensor, y_true: torch.Tensor, 
           y_pred: torch.Tensor, lr: float) -> None:
    """
    Update the model parameters.

    Args:
       x: Input tensor of shape (n_samples, n_features).
       y_true: Target tensor of shape (n_samples, n_classes).
       y_pred: Predicted output tensor of shape (n_samples, n_classes).
       lr: Learning rate. 
    """
    # cross entropy der
    delta = -(y_true / y_pred) / len(y_true)
    # softmax der
    delta = y_pred * (delta - (delta * y_pred).sum(axis=1, keepdims=True))
    # weighted sum der
    self.b -= lr * delta.sum(axis=0)
    self.w -= lr * (x.T @ delta)

metric: accuracy¶

@add_to_class(SoftmaxClassifier)
def accuracy(self, y_true, y_pred) -> float:
    preds = y_pred.argmax(axis=-1)
    compare = (y_true.argmax(axis=-1) == preds).type(torch.float32)
    return compare.mean().item()

fit (train)¶

@add_to_class(SoftmaxClassifier)
def fit(self, x_train: torch.Tensor, y_train: torch.Tensor, 
        epochs: int, lr: float, batch_size: int, 
        x_valid: torch.Tensor, y_valid: torch.Tensor) -> None:
    """
    Fit the model using gradient descent.

    Args:
        x_train: Input tensor of shape (n_samples, num_features).
        y_train: Target tensor one hot of shape (n_samples, n_classes).
        epochs: Number of epochs to train.
        lr: learning rate).
        batch_size: Int number of batch.
        x_valid: Input tensor of shape (n_valid_samples, num_features).
        y_valid: Input tensor one hot of shape (n_valid_samples, n_valid_classes).
    """
    for epoch in range(epochs):
        loss = []
        for batch in range(0, len(y_train), batch_size):
            batch_end = batch + batch_size

            y_pred = self.predict(x_train[batch:batch_end])
            loss.append(self.evaluate(
                x_train[batch:batch_end], 
                y_train[batch:batch_end]
            ))

            self.update(
                x_train[batch:batch_end], 
                y_train[batch:batch_end], 
                y_pred, lr
            )

        loss = round(sum(loss) / len(loss), 4)
        loss_v = round(self.evaluate(x_valid, y_valid), 4)
        acc = round(self.accuracy(y_valid, self.predict(x_valid)), 4)
        print(f'epoch: {epoch} - CE: {loss} - CE_v: {loss_v} - acc_v: {acc}')

Scratch vs nn¶

nn model¶

Important: nn.CrossEntropyLoss applies Softmax to input

class TorchSoftmax(nn.Module):
    def __init__(self, n_features, n_out_features):
        super(TorchSoftmax, self).__init__()
        self.layer = nn.Linear(n_features, n_out_features, device=device)
        self.soft = nn.Softmax(dim=1)
        self.loss = nn.CrossEntropyLoss()

    def forward(self, x):
        z = self.layer(x)
        return self.soft(z)
    
    def evaluate(self, x, y):
        self.eval()
        with torch.no_grad():
            y_pred = self.layer(x)
            # do not use self.soft because nn.CrossEntropyLoss already uses softmax
            return self.loss(y_pred, y).item()
    
    def fit(self, x, y, epochs, lr, batch_size, x_valid, y_valid):
        optimizer = torch.optim.SGD(self.parameters(), lr=lr)
        for epoch in range(epochs):
            loss_t = []
            for batch in range(0, len(y), batch_size):
                batch_end = batch + batch_size

                y_pred = self.layer(x[batch:batch_end])
                loss = self.loss(y_pred, y[batch:batch_end])
                loss_t.append(loss.item())

                optimizer.zero_grad()
                loss.backward()
                optimizer.step()

            loss_t = round(sum(loss_t) / len(loss_t), 4)
            loss_v = round(self.evaluate(x_valid, y_valid), 4)
            print(f'epoch: {epoch} - CE: {loss_t} - CE_v: {loss_v}')

torch_model = TorchSoftmax(N, CLASSES)

scratch model¶

model = SoftmaxClassifier(N, CLASSES)

evals¶

import MAPE modified¶

# This cell imports torch_mape 
# if you are running this notebook locally 
# or from Google Colab.

import os
import sys

module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
    sys.path.append(module_path)

try:
    from tools.torch_metrics import torch_mape as mape
    print('mape imported locally.')
except ModuleNotFoundError:
    import subprocess

    repo_url = 'https://raw.githubusercontent.com/PilotLeoYan/inside-deep-learning/main/content/tools/torch_metrics.py'
    local_file = 'torch_metrics.py'
    
    subprocess.run(['wget', repo_url, '-O', local_file], check=True)
    try:
        from torch_metrics import torch_mape as mape # type: ignore
        print('mape imported from GitHub.')
    except Exception as e:
        print(e)

mape imported locally.

predict¶

mape(
    model.predict(X_valid),
    torch_model(X_valid)
)

1251.541284177607

copy parameters¶

model.copy_params(torch_model.layer)
parameters = (model.b.clone(), model.w.clone())

predict after copy parameters¶

mape(
    model.predict(X_valid),
    torch_model(X_valid)
)

3.1321066736458506e-15

CE¶

mape(
    model.evaluate(X_valid, Y_valid),
    torch_model.evaluate(X_valid, Y_valid)
)

0.0

train¶

LR = 0.01
EPOCHS = 16
BATCH = len(X_train) // 3

torch_model.fit(
    X_train, Y_train, 
    EPOCHS, LR, BATCH, 
    X_valid, Y_valid
)

epoch: 0 - CE: 1.6184 - CE_v: 1.2516
epoch: 1 - CE: 1.5201 - CE_v: 1.2035
epoch: 2 - CE: 1.4288 - CE_v: 1.1591
epoch: 3 - CE: 1.3446 - CE_v: 1.1185
epoch: 4 - CE: 1.2675 - CE_v: 1.0813
epoch: 5 - CE: 1.1973 - CE_v: 1.0475
epoch: 6 - CE: 1.1338 - CE_v: 1.0169
epoch: 7 - CE: 1.0764 - CE_v: 0.989
epoch: 8 - CE: 1.0248 - CE_v: 0.9638
epoch: 9 - CE: 0.9784 - CE_v: 0.941
epoch: 10 - CE: 0.9367 - CE_v: 0.9203
epoch: 11 - CE: 0.8991 - CE_v: 0.9015
epoch: 12 - CE: 0.8653 - CE_v: 0.8844

epoch: 13 - CE: 0.8347 - CE_v: 0.8688
epoch: 14 - CE: 0.8069 - CE_v: 0.8546
epoch: 15 - CE: 0.7818 - CE_v: 0.8416

model.fit(
    X_train, Y_train, 
    EPOCHS, LR, BATCH, 
    X_valid, Y_valid
)

epoch: 0 - CE: 1.6184 - CE_v: 1.2516 - acc_v: 0.3979
epoch: 1 - CE: 1.5201 - CE_v: 1.2035 - acc_v: 0.4073
epoch: 2 - CE: 1.4288 - CE_v: 1.1591 - acc_v: 0.4199
epoch: 3 - CE: 1.3446 - CE_v: 1.1185 - acc_v: 0.4312
epoch: 4 - CE: 1.2675 - CE_v: 1.0813 - acc_v: 0.4461
epoch: 5 - CE: 1.1973 - CE_v: 1.0475 - acc_v: 0.4634

epoch: 6 - CE: 1.1338 - CE_v: 1.0169 - acc_v: 0.4845
epoch: 7 - CE: 1.0764 - CE_v: 0.989 - acc_v: 0.5066
epoch: 8 - CE: 1.0248 - CE_v: 0.9638 - acc_v: 0.5276
epoch: 9 - CE: 0.9784 - CE_v: 0.941 - acc_v: 0.546

epoch: 10 - CE: 0.9367 - CE_v: 0.9203 - acc_v: 0.5611
epoch: 11 - CE: 0.8991 - CE_v: 0.9015 - acc_v: 0.5739
epoch: 12 - CE: 0.8653 - CE_v: 0.8844 - acc_v: 0.5839
epoch: 13 - CE: 0.8347 - CE_v: 0.8688 - acc_v: 0.5956
epoch: 14 - CE: 0.8069 - CE_v: 0.8546 - acc_v: 0.6025
epoch: 15 - CE: 0.7818 - CE_v: 0.8416 - acc_v: 0.6097

predict after train¶

mape(
    model.predict(X_valid),
    torch_model.forward(X_valid)
)

9.90849577738569e-15

weight¶

mape(
    model.w.clone(),
    torch_model.layer.weight.detach().T
)

9.33457522819254e-15

bias¶

mape(
    model.b.clone(),
    torch_model.layer.bias.detach()
)

4.524992525368498e-15

Compute gradient with einsum¶

Gradient descent is

\frac{\partial L}{\partial \mathbf{W}} = \frac{\partial L}{\partial \mathbf{\Sigma}} \frac{\partial \mathbf{\Sigma}}{\partial \mathbf{Z}} \frac{\partial \mathbf{Z}}{\partial \mathbf{W}}

(20)

and

\frac{\partial L}{\partial \mathbf{b}} = \frac{\partial L}{\partial \mathbf{\Sigma}} \frac{\partial \mathbf{\Sigma}}{\partial \mathbf{Z}} \frac{\partial \mathbf{Z}}{\partial \mathbf{b}}

(21)

where their shapes are

\begin{align*} \frac{\partial L} {\partial \mathbf{W}} &\in \mathbb{R}^{n \times n_{1}} \\ \frac{\partial L} {\partial \mathbf{b}} &\in \mathbb{R}^{n_{1}} \\ \frac{\partial L} {\partial \mathbf{\Sigma}} &\in \mathbb{R}^{m \times n_{1}} \\ \frac{\partial \mathbf{\Sigma}} {\partial \mathbf{Z}} &\in \mathbb{R}^{(m \times n_{1}) \times (m \times n_{1})} \\ \frac{\partial \mathbf{Z}} {\partial \mathbf{W}} &\in \mathbb{R}^{(m \times n_{1}) \times (n \times n_{1})} \\ \frac{\partial \mathbf{Z}} {\partial \mathbf{b}} &\in \mathbb{R}^{(m \times n_{1}) \times n_{1}} \end{align*}

(22)

Then we have 2 cases

\frac{\partial \mathbf{\Sigma}(\mathbf{Z})_{i,:}} {\partial \mathbf{Z}_{p=i,:}}

(23)

and

\frac{\partial \mathbf{\Sigma}(\mathbf{Z})_{i,:}} {\partial \mathbf{Z}_{p\neq i,:}}

(24)

First case

\frac{\partial \mathbf{\Sigma}(\mathbf{Z})_{i,:}} {\partial \mathbf{Z}_{p=i,:}} = \text{diag}(\sigma(\mathbf{Z}_{i,:})) - \sigma(\mathbf{Z}_{i,:}) \sigma(\mathbf{Z}_{i,:})^\top

(25)

Second case

\frac{\partial \mathbf{\Sigma}(\mathbf{Z})_{i,:}} {\partial \mathbf{Z}_{p \neq i,:}} = \mathbf{0}

(26)

Weighted sum derivative

\frac{\partial \mathbf{Z}}{\partial \mathbf{W}} = \mathbb{I} \otimes \mathbf{X}

(27)

\frac{\partial z_{ij}}{\partial b_{p}} = \begin{cases} 1 & \text{if } j=p \\ 0 & \text{if } j\neq p \end{cases}

(28)

for all $i = 1, \ldots, m$ and $j, p = 1, \ldots, n_{1}$

therefore using Einstein summation

\begin{align*} {\color{Orange} {\frac{\partial L}{\partial \mathbf{Z}}}} &= {\color{Lime} {\frac{\partial L}{\partial \mathbf{\Sigma}}}} {\color{Cyan} {\frac{\partial \mathbf{\Sigma}}{\partial \mathbf{Z}}}} \\ &\in \mathbb{R}^{ {\color{Lime} {(m \times n_{1})}} \times {\color{Cyan} {(m \times n_{1} \times m \times n_{1})}}} \\ &\in \mathbb{R}^{\color{Orange} {{m \times n_{1}}}} \end{align*}

(29)

\begin{align*} {\color{Magenta} {\frac{\partial L}{\partial \mathbf{b}}}} &= {\color{Orange} {\frac{\partial L}{\partial \mathbf{Z}}}} {\color{Cyan} {\frac{\partial \mathbf{Z}}{\partial \mathbf{b}}}} \\ &\in \mathbb{R}^{ {\color{Orange} {(m \times n_{1})}} \times {\color{Cyan} {(m \times n_{1} \times n_{1})}}} \\ &\in \mathbb{R}^{\color{Magenta} {n_{1}}} \end{align*}

(30)

and

\begin{align*} {\color{Magenta} {\frac{\partial L}{\partial \mathbf{W}}}} &= {\color{Orange} {\frac{\partial L}{\partial \mathbf{Z}}}} {\color{Cyan} {\frac{\partial \mathbf{Z}}{\partial \mathbf{W}}}} \\ &\in \mathbb{R}^{ {\color{Orange} {(m \times n_{1})}} \times {\color{Cyan} {(m \times n_{1} \times n \times n_{1})}}} \\ &\in \mathbb{R}^{\color{Magenta} {n \times n_{1}}} \end{align*}

(31)

Model¶

class EinsumSoftmaxClassifier(SoftmaxClassifier):
    def update(self, x: torch.Tensor, y_true: torch.Tensor,
           y_pred: torch.Tensor, lr: float) -> None:
        """
        Update the model parameters.

        Args:
            x: Input tensor of shape (n_samples, n_features).
            y_true: Target tensor of shape (n_samples, n_classes).
            y_pred: Predicted output tensor of shape (n_samples, n_classes).
            lr: Learning rate. 
        """
        m, n_classes = y_true.shape
        # cross entropy der
        delta = -(y_true / y_pred) / m
        # softmax der
        diag_a = torch.diag_embed(y_pred)
        outer_a = torch.einsum('ij,ik->ijk', y_pred, y_pred) 
        soft_der = torch.zeros(
            (m, n_classes, m, n_classes), 
            dtype=y_pred.dtype, 
            device=device
        )
        idx = torch.arange(m, device=device)
        soft_der[idx, :, idx, :] = diag_a - outer_a
        delta = torch.einsum('pq,pqij->ij', delta, soft_der)
        # weighted sum der
        self.b -= lr * delta.sum(axis=0)
        
        identity = torch.eye(n_classes, device=device)
        w_der = torch.kron(
            x.unsqueeze(1).unsqueeze(3), 
            identity.unsqueeze(0).unsqueeze(2)
        )
        w_der = torch.einsum('pq,pqij->ij', delta, w_der)
        self.w -= lr * w_der

einsum_model = EinsumSoftmaxClassifier(N, CLASSES)
einsum_model.b.copy_(parameters[0])
einsum_model.w.copy_(parameters[1])

tensor([[ 0.1326, -0.4085,  0.3936],
        [ 0.4109,  0.3352, -0.0413],
        [ 0.4252, -0.0872, -0.3827],
        [-0.2778, -0.3890, -0.1415],
        [ 0.3257, -0.3748, -0.4078]])

einsum_model.fit(
    X_train, Y_train, 
    EPOCHS, LR, BATCH, 
    X_valid, Y_valid
)

epoch: 0 - CE: 1.6184 - CE_v: 1.2516 - acc_v: 0.3979
epoch: 1 - CE: 1.5201 - CE_v: 1.2035 - acc_v: 0.4073
epoch: 2 - CE: 1.4288 - CE_v: 1.1591 - acc_v: 0.4199
epoch: 3 - CE: 1.3446 - CE_v: 1.1185 - acc_v: 0.4312
epoch: 4 - CE: 1.2675 - CE_v: 1.0813 - acc_v: 0.4461
epoch: 5 - CE: 1.1973 - CE_v: 1.0475 - acc_v: 0.4634

epoch: 6 - CE: 1.1338 - CE_v: 1.0169 - acc_v: 0.4845
epoch: 7 - CE: 1.0764 - CE_v: 0.989 - acc_v: 0.5066

epoch: 8 - CE: 1.0248 - CE_v: 0.9638 - acc_v: 0.5276
epoch: 9 - CE: 0.9784 - CE_v: 0.941 - acc_v: 0.546
epoch: 10 - CE: 0.9367 - CE_v: 0.9203 - acc_v: 0.5611
epoch: 11 - CE: 0.8991 - CE_v: 0.9015 - acc_v: 0.5739
epoch: 12 - CE: 0.8653 - CE_v: 0.8844 - acc_v: 0.5839
epoch: 13 - CE: 0.8347 - CE_v: 0.8688 - acc_v: 0.5956
epoch: 14 - CE: 0.8069 - CE_v: 0.8546 - acc_v: 0.6025
epoch: 15 - CE: 0.7818 - CE_v: 0.8416 - acc_v: 0.6097

mape(
    einsum_model.w.clone(),
    torch_model.layer.weight.detach().T
)

4.057167691616559e-15

mape(
    einsum_model.b.clone(),
    torch_model.layer.bias.detach()
)

4.524992525368498e-15