Gradients and activations functions December 9, 2025
In this notebook we will explore the derivatives of
different activation functions such as ReLU, Sigmoid and Tanh.
In addition, we will explore the derivatives of the dense layer,
some of which are already known, but there is a new derivative that needs to be explored.
from autograd import jacobian, numpy as np
from platform import python_version
python_version()# This cell imports numpy_mape
# if you are running this notebook locally
# or from Google Colab.
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
try:
from tools.numpy_metrics import np_mape as mape
print('mape imported locally.')
except ModuleNotFoundError:
import subprocess
repo_url = 'https://raw.githubusercontent.com/PilotLeoYan/inside-deep-learning/main/content/tools/numpy_metrics.py'
local_file = 'numpy_metrics.py'
subprocess.run(['wget', repo_url, '-O', local_file], check=True)
try:
from numpy_metrics import np_mape as mape # type: ignore
print('mape imported from GitHub.')
except Exception as e:
print(e)M: int = 100 # number of samples
N: int = 8 # number of input features
NO: int = 4 # number of output features
X = np.random.randn(M, N)
X.shapeW ( k ) ∈ R n k − 1 × n k b ( k ) ∈ R n k \begin{align*}
\mathbf{W}^{(k)} &\in \mathbb{R}^{n_{k-1} \times n_{k}} \\
\mathbf{b}^{(k)} &\in \mathbb{R}^{n_{k}}
\end{align*} W ( k ) b ( k ) ∈ R n k − 1 × n k ∈ R n k bias: np.ndarray = np.random.randn(NO)
bias.shapeweight: np.ndarray = np.random.randn(N, NO)
weight.shapeZ ( k ) ( A ( k − 1 ) ) = A ( k − 1 ) W ( k ) + b ( k ) Z ( k ) : R m × n k − 1 → R m × n k \mathbf{Z}^{(k)} (\mathbf{A}^{(k-1)}) =
\mathbf{A}^{(k-1)} \mathbf{W}^{(k)} + \mathbf{b}^{(k)} \\
\mathbf{Z}^{(k)} : \mathbb{R}^{m \times n_{k-1}}
\rightarrow \mathbb{R}^{m \times n_{k}} Z ( k ) ( A ( k − 1 ) ) = A ( k − 1 ) W ( k ) + b ( k ) Z ( k ) : R m × n k − 1 → R m × n k def weighted_sum(input: np.ndarray, weight: np.ndarray,
bias: np.ndarray) -> np.ndarray:
return np.matmul(input, weight) + bias
z = weighted_sum(X, weight, bias)
z.shapeFor any activation function
A ( k ) ( Z ( k ) ) = f ( Z ( k ) ) A ( k ) : R m × n k → R m × n k \mathbf{A}^{(k)} (\mathbf{Z}^{(k)}) =
f(\mathbf{Z}^{(k)}) \\
\mathbf{A}^{(k)}: \mathbb{R}^{m \times n_{k}}
\rightarrow \mathbb{R}^{m \times n_{k}} A ( k ) ( Z ( k ) ) = f ( Z ( k ) ) A ( k ) : R m × n k → R m × n k ReLU ( z ) = max ( z , 0 ) ∈ R \text{ReLU}(z) = \max(z, 0) \in \mathbb{R} ReLU ( z ) = max ( z , 0 ) ∈ R where z ∈ R z \in \mathbb{R} z ∈ R
ReLU ( Z ( k ) ) = [ ReLU ( z 11 ( k ) ) ⋯ ReLU ( z 1 n k ( k ) ) ⋮ ⋱ ⋮ ReLU ( z m 1 ( k ) ) ⋯ ReLU ( z m n k ( k ) ) ] \text{ReLU} (\mathbf{Z}^{(k)}) =
\begin{bmatrix}
\text{ReLU}(z_{11}^{(k)}) & \cdots & \text{ReLU}(z_{1n_{k}}^{(k)}) \\
\vdots & \ddots & \vdots \\
\text{ReLU}(z_{m1}^{(k)}) & \cdots & \text{ReLU}(z_{mn_{k}}^{(k)})
\end{bmatrix} ReLU ( Z ( k ) ) = ⎣ ⎡ ReLU ( z 11 ( k ) ) ⋮ ReLU ( z m 1 ( k ) ) ⋯ ⋱ ⋯ ReLU ( z 1 n k ( k ) ) ⋮ ReLU ( z m n k ( k ) ) ⎦ ⎤ def relu(z: np.ndarray) -> np.ndarray:
return z * (z > 0)
relu_pred = relu(z)
relu_pred.shapeSigmoid ( z ) = 1 1 + exp ( − z ) \text{Sigmoid}(z) = \frac{1}{1 + \exp(-z)} Sigmoid ( z ) = 1 + exp ( − z ) 1 Sigmoid ( Z ( k ) ) = [ Sigmoid ( z 11 ( k ) ) ⋯ Sigmoid ( z 1 n k ( k ) ) ⋮ ⋱ ⋮ Sigmoid ( z m 1 ( k ) ) ⋯ Sigmoid ( z m n k ( k ) ) ] \text{Sigmoid} (\mathbf{Z}^{(k)}) =
\begin{bmatrix}
\text{Sigmoid}(z_{11}^{(k)}) & \cdots & \text{Sigmoid}(z_{1n_{k}}^{(k)}) \\
\vdots & \ddots & \vdots \\
\text{Sigmoid}(z_{m1}^{(k)}) & \cdots & \text{Sigmoid}(z_{mn_{k}}^{(k)})
\end{bmatrix} Sigmoid ( Z ( k ) ) = ⎣ ⎡ Sigmoid ( z 11 ( k ) ) ⋮ Sigmoid ( z m 1 ( k ) ) ⋯ ⋱ ⋯ Sigmoid ( z 1 n k ( k ) ) ⋮ Sigmoid ( z m n k ( k ) ) ⎦ ⎤ def sigmoid(z: np.ndarray) -> np.ndarray:
return 1 / (1 + np.exp(-z))
sigmoid_pred = sigmoid(z)
sigmoid_pred.shapetanh ( z ) = 1 − exp ( − 2 z ) 1 + exp ( − 2 z ) \tanh(z) = \frac{1 - \exp(-2 z)}{1 + \exp(-2 z)} tanh ( z ) = 1 + exp ( − 2 z ) 1 − exp ( − 2 z ) tanh ( Z ( k ) ) = [ tanh ( z 11 ( k ) ) ⋯ tanh ( z 1 n k ( k ) ) ⋮ ⋱ ⋮ tanh ( z m 1 ( k ) ) ⋯ tanh ( z m n k ( k ) ) ] \tanh (\mathbf{Z}^{(k)}) =
\begin{bmatrix}
\tanh(z_{11}^{(k)}) & \cdots & \tanh(z_{1n_{k}}^{(k)}) \\
\vdots & \ddots & \vdots \\
\tanh(z_{m1}^{(k)}) & \cdots & \tanh(z_{mn_{k}}^{(k)})
\end{bmatrix} tanh ( Z ( k ) ) = ⎣ ⎡ tanh ( z 11 ( k ) ) ⋮ tanh ( z m 1 ( k ) ) ⋯ ⋱ ⋯ tanh ( z 1 n k ( k ) ) ⋮ tanh ( z m n k ( k ) ) ⎦ ⎤ def tanh(z: np.ndarray) -> np.ndarray:
exp = np.exp(-2 * z)
return (1 - exp) / (1 + exp)
tanh_pred = tanh(z)
tanh_pred.shapeactivation function gradients ¶ For any activation function A \mathbf{A} A
∂ A ( k ) ∂ Z ( k ) ∈ R ( m × n k ) × ( m × n k ) \frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}} \in
\mathbb{R}^{(m \times n_{k}) \times (m \times n_{k})} ∂ Z ( k ) ∂ A ( k ) ∈ R ( m × n k ) × ( m × n k ) relu_grad = jacobian(relu)(z)
relu_grad.shaped max ( z , 0 ) d z = { 1 if z > 0 0 if z ≤ 0 \frac{\mathrm{d} \max(z,0)}{\mathrm{d} z} =
\begin{cases}
1 & \text{if } z > 0 \\
0 & \text{if } z \leq 0
\end{cases} d z d max ( z , 0 ) = { 1 0 if z > 0 if z ≤ 0 ∂ a p q ( k ) ∂ z i j ( k ) = { ∂ a i j ( k ) ∂ z i j ( k ) if p = i , q = j 0 otherwise \frac{\partial a_{pq}^{(k)}
}{\partial z_{ij}^{(k)}} =
\begin{cases}
\frac{\partial a_{ij}^{(k)}}
{\partial z_{ij}^{(k)}} & \text{ if } p=i, q=j \\
0 & \text{ otherwise}
\end{cases} ∂ z ij ( k ) ∂ a pq ( k ) = ⎩ ⎨ ⎧ ∂ z ij ( k ) ∂ a ij ( k ) 0 if p = i , q = j otherwise for all p , i = 1 , … , m p, i = 1, \ldots, m p , i = 1 , … , m q , j = 1 , … , n k q, j = 1, \ldots, n_{k} q , j = 1 , … , n k
∂ a i j ( k ) ∂ z i j ( k ) = { 1 if z i j ( k ) > 0 0 if z i j ( k ) ≤ 0 \frac{\partial a_{ij}^{(k)}}
{\partial z_{ij}^{(k)}} =
\begin{cases}
1 & \text{if } z_{ij}^{(k)} > 0 \\
0 & \text{if } z_{ij}^{(k)} \leq 0
\end{cases} ∂ z ij ( k ) ∂ a ij ( k ) = { 1 0 if z ij ( k ) > 0 if z ij ( k ) ≤ 0 we can take advantage of the same activation output
∂ a i j ( k ) ∂ z i j ( k ) = { 1 if a i j ( k ) > 0 0 if a i j ( k ) ≤ 0 \frac{\partial a_{ij}^{(k)}}
{\partial z_{ij}^{(k)}} =
\begin{cases}
1 & \text{if } a_{ij}^{(k)} > 0 \\
0 & \text{if } a_{ij}^{(k)} \leq 0
\end{cases} ∂ z ij ( k ) ∂ a ij ( k ) = { 1 0 if a ij ( k ) > 0 if a ij ( k ) ≤ 0 def relu_jacobian(relu_out: np.ndarray) -> np.ndarray:
m, n = relu_out.shape # m samples, n features
out = np.zeros((m, n, m, n))
for i in range(m):
for j in range(n):
out[i, j, i, j] = 1 if relu_out[i, j] > 0 else 0
return out
my_relu_grad = relu_jacobian(relu_pred)
my_relu_grad.shapemape(
my_relu_grad,
relu_grad
)sigmoid_grad = jacobian(sigmoid)(z)
sigmoid_grad.shaped Sigmoid d z = Sigmoid ( z ) ( 1 − Sigmoid ( z ) ) \frac{\mathrm{d} \text{Sigmoid}}{\mathrm{d} z} =
\text{Sigmoid}(z) \left(
1 - \text{Sigmoid}(z)
\right) d z d Sigmoid = Sigmoid ( z ) ( 1 − Sigmoid ( z ) ) ∂ a p q ( k ) ∂ z i j ( k ) = { a i j ( k ) ( 1 − a i j ( k ) ) if p = i , q = j 0 otherwise \frac{\partial a_{pq}^{(k)}}
{\partial z_{ij}^{(k)}} =
\begin{cases}
a_{ij}^{(k)} (1 - a_{ij}^{(k)})
& \text{if }p = i, q = j \\
0 & \text{otherwise}
\end{cases} ∂ z ij ( k ) ∂ a pq ( k ) = { a ij ( k ) ( 1 − a ij ( k ) ) 0 if p = i , q = j otherwise def sigmoid_jacobian(sigm_out: np.ndarray) -> np.ndarray:
m, n = sigm_out.shape # m samples, n features
out = np.zeros((m, n, m, n))
for i in range(m):
for j in range(n):
out[i, j, i, j] = sigm_out[i, j] * (1 - sigm_out[i, j])
return out
my_sigmoid_grad = sigmoid_jacobian(sigmoid_pred)
my_sigmoid_grad.shapemape(
my_sigmoid_grad,
sigmoid_grad
)d tanh d z = 1 − tanh 2 ( z ) \frac{\mathrm{d} \tanh}{\mathrm{d} z} =
1 - \tanh^{2}(z) d z d tanh = 1 − tanh 2 ( z ) ∂ a p q ( k ) ∂ z i j ( k ) = { 1 − ( a i j ( k ) ) 2 if p = i , q = j 0 otherwise \frac{\partial a_{pq}^{(k)}}
{\partial z_{ij}^{(k)}} =
\begin{cases}
1 - (a_{ij}^{(k)})^{2} & \text{if } p = i, q = j \\
0 & \text{otherwise}
\end{cases} ∂ z ij ( k ) ∂ a pq ( k ) = { 1 − ( a ij ( k ) ) 2 0 if p = i , q = j otherwise tanh_grad = jacobian(tanh)(z)
tanh_grad.shapedef tanh_jacobian(tanh_out: np.ndarray) -> np.ndarray:
m, n = tanh_out.shape # m samples, n features
out = np.zeros((m, n, m, n))
for i in range(m):
for j in range(n):
out[i, j, i, j] = 1 - tanh_out[i, j] ** 2
return out
my_tanh_grad = tanh_jacobian(tanh_pred)
my_tanh_grad.shapemape(
my_tanh_grad,
tanh_grad
)gradients with loss function ¶ ∂ L ∂ A ( k ) , ∂ L ∂ W ( k ) , ∂ L ∂ b ( k ) \frac{\partial L}{\partial \mathbf{A}^{(k)}},
\frac{\partial L}{\partial \mathbf{W}^{(k)}},
\frac{\partial L}{\partial \mathbf{b}^{(k)}} ∂ A ( k ) ∂ L , ∂ W ( k ) ∂ L , ∂ b ( k ) ∂ L For any loss function L L L
L ( Y ^ ) = ∑ i = 1 m ∑ j = 1 n o y ^ i j 2 L(\hat{\mathbf{Y}}) =
\sum_{i=1}^{m}
\sum_{j=1}^{n_{\text{o}}}
\hat{y}_{ij}^{2} L ( Y ^ ) = i = 1 ∑ m j = 1 ∑ n o y ^ ij 2 def loss(y_pred: np.ndarray) -> float:
return np.sum(y_pred ** 2)
∂ L ∂ Y ^ = 2 Y ^ \frac{\partial L}
{\partial \hat{\mathbf{Y}}} =
2 \hat{\mathbf{Y}} ∂ Y ^ ∂ L = 2 Y ^ activation function gradients ¶ ∂ L ∂ Z ( k ) = ∂ L ∂ A ( k ) ∂ A ( k ) ∂ Z ( k ) = Δ ∂ A ( k ) ∂ Z ( k ) \begin{align*}
\frac{\partial L}{\partial \mathbf{Z}^{(k)}} &=
{\color{Orange} {\frac{\partial L}{\partial \mathbf{A}^{(k)}}}}
{\color{Cyan} {\frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}}}} \\
&= {\color{Orange} {\mathbf{\Delta}}}
{\color{Cyan} {\frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}}}}
\end{align*} ∂ Z ( k ) ∂ L = ∂ A ( k ) ∂ L ∂ Z ( k ) ∂ A ( k ) = Δ ∂ Z ( k ) ∂ A ( k ) loss_relu_grad = jacobian(lambda z: loss(relu(z)))(z)
loss_relu_grad.shapedelta_relu = jacobian(loss)(relu_pred)
delta_relu.shape∂ L ∂ z p q ( k ) = ∑ i = 0 m ∑ j = 0 n o ∂ L ∂ a i j ( k ) ∂ a i j ( k ) ∂ z p q ( k ) \frac{\partial L}{\partial z^{(k)}_{pq}} =
\sum_{i=0}^{m} \sum_{j=0}^{n_{o}}
\frac{\partial L}{\partial a_{ij}^{(k)}}
\frac{\partial a_{ij}^{(k)}}{\partial z_{pq}^{(k)}} ∂ z pq ( k ) ∂ L = i = 0 ∑ m j = 0 ∑ n o ∂ a ij ( k ) ∂ L ∂ z pq ( k ) ∂ a ij ( k ) For the case i = p i=p i = p j = q j=q j = q
∂ a p q ( k ) ∂ z p q ( k ) = { 1 if z p q ( k ) > 0 0 if z p q ( k ) ≤ 0 \frac{\partial a_{pq}^{(k)}}
{\partial z_{pq}^{(k)}} =
\begin{cases}
1 & \text{if } z_{pq}^{(k)} > 0 \\
0 & \text{if } z_{pq}^{(k)} \leq 0
\end{cases} ∂ z pq ( k ) ∂ a pq ( k ) = { 1 0 if z pq ( k ) > 0 if z pq ( k ) ≤ 0 For the case i ≠ p i \neq p i = p j ≠ q j \neq q j = q
∂ a i j ( k ) ∂ z p q ( k ) = 0 \frac{\partial a_{ij}^{(k)}}
{\partial z_{pq}^{(k)}} = 0 ∂ z pq ( k ) ∂ a ij ( k ) = 0 ∂ L ∂ z p q ( k ) = ∂ L ∂ a p q ( k ) ∂ a p q ( k ) ∂ z p q ( k ) = δ p q { 1 if a p q ( k ) > 0 0 if a p q ( k ) ≤ 0 \begin{align*}
\frac{\partial L}{\partial z^{(k)}_{pq}} &=
\frac{\partial L}{\partial a_{pq}^{(k)}}
\frac{\partial a_{pq}^{(k)}}{\partial z_{pq}^{(k)}} \\
&= \delta_{pq} \begin{cases}
1 & \text{if } a_{pq}^{(k)} > 0 \\
0 & \text{if } a_{pq}^{(k)} \leq 0
\end{cases}
\end{align*} ∂ z pq ( k ) ∂ L = ∂ a pq ( k ) ∂ L ∂ z pq ( k ) ∂ a pq ( k ) = δ pq { 1 0 if a pq ( k ) > 0 if a pq ( k ) ≤ 0 for all p = m p = m p = m q = n k q = n_{k} q = n k
∂ L ∂ Z ( k ) = ∂ L ∂ A ( k ) ⊙ ∂ A ( k ) ∂ Z ( k ) = Δ ⊙ ( A ( k ) > 0 ) \begin{align*}
\frac{\partial L}{\partial \mathbf{Z}^{(k)}} &=
\frac{\partial L}{\partial \mathbf{A}^{(k)}}
\odot
\frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}} \\ &=
\mathbf{\Delta} \odot
\left(
\mathbf{A}^{(k)} > 0
\right)
\end{align*} ∂ Z ( k ) ∂ L = ∂ A ( k ) ∂ L ⊙ ∂ Z ( k ) ∂ A ( k ) = Δ ⊙ ( A ( k ) > 0 ) Note : Remember that we can use the same result of the
activation function for backpropagation.
def loss_relu_der(delta: np.ndarray, relu_out: np.ndarray) -> np.ndarray:
return np.multiply(delta, 1 * (relu_out > 0))
my_loss_relu_grad = loss_relu_der(delta_relu, relu_pred)
my_loss_relu_grad.shapemape(
my_loss_relu_grad,
loss_relu_grad
)loss_sigmoid_grad = jacobian(lambda z: loss(sigmoid(z)))(z)
loss_sigmoid_grad.shapedelta_sigmoid = jacobian(loss)(sigmoid_pred)
delta_sigmoid.shape∂ L ∂ z p q ( k ) = ∑ i = 0 m ∑ j = 0 n o ∂ L ∂ a i j ( k ) ∂ a i j ( k ) ∂ z p q ( k ) \frac{\partial L}{\partial z^{(k)}_{pq}} =
\sum_{i=0}^{m} \sum_{j=0}^{n_{o}}
\frac{\partial L}{\partial a_{ij}^{(k)}}
\frac{\partial a_{ij}^{(k)}}{\partial z_{pq}^{(k)}} ∂ z pq ( k ) ∂ L = i = 0 ∑ m j = 0 ∑ n o ∂ a ij ( k ) ∂ L ∂ z pq ( k ) ∂ a ij ( k ) For the case i = p i=p i = p j = q j=q j = q
∂ a p q ( k ) ∂ z p q ( k ) = a p q ( k ) ( 1 − a p q ( k ) ) \frac{\partial a_{pq}^{(k)}}
{\partial z_{pq}^{(k)}} =
a_{pq}^{(k)} \left(
1 - a_{pq}^{(k)}
\right) ∂ z pq ( k ) ∂ a pq ( k ) = a pq ( k ) ( 1 − a pq ( k ) ) For the case i ≠ p i \neq p i = p j ≠ q j \neq q j = q
∂ a i j ( k ) ∂ z p q ( k ) = 0 \frac{\partial a_{ij}^{(k)}}
{\partial z_{pq}^{(k)}} = 0 ∂ z pq ( k ) ∂ a ij ( k ) = 0 ∂ L ∂ z p q ( k ) = ∂ L ∂ a p q ( k ) ∂ a p q ( k ) ∂ z p q ( k ) = δ p q ( a p q ( k ) ( 1 − a p q ( k ) ) ) \begin{align*}
\frac{\partial L}{\partial z^{(k)}_{pq}} &=
\frac{\partial L}{\partial a_{pq}^{(k)}}
\frac{\partial a_{pq}^{(k)}}{\partial z_{pq}^{(k)}} \\
&= \delta_{pq} \left(
a_{pq}^{(k)} \left(
1 - a_{pq}^{(k)}
\right)
\right)
\end{align*} ∂ z pq ( k ) ∂ L = ∂ a pq ( k ) ∂ L ∂ z pq ( k ) ∂ a pq ( k ) = δ pq ( a pq ( k ) ( 1 − a pq ( k ) ) ) for all p = m p = m p = m q = n k q = n_{k} q = n k
∂ L ∂ Z ( k ) = ∂ L ∂ A ( k ) ⊙ ∂ A ( k ) ∂ Z ( k ) = Δ ⊙ ( A ( k ) ( 1 − A ( k ) ) ) \begin{align*}
\frac{\partial L}{\partial \mathbf{Z}^{(k)}} &=
\frac{\partial L}{\partial \mathbf{A}^{(k)}}
\odot
\frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}} \\ &=
\mathbf{\Delta} \odot
\left(
\mathbf{A}^{(k)} \left(
\mathbf{1} - \mathbf{A}^{(k)}
\right)
\right)
\end{align*} ∂ Z ( k ) ∂ L = ∂ A ( k ) ∂ L ⊙ ∂ Z ( k ) ∂ A ( k ) = Δ ⊙ ( A ( k ) ( 1 − A ( k ) ) ) def loss_sigmoid_der(delta: np.ndarray, sigm_out: np.ndarray) -> np.ndarray:
return np.multiply(delta, sigm_out * (1 - sigm_out))
my_loss_sigmoid_grad = loss_sigmoid_der(delta_sigmoid, sigmoid_pred)
my_loss_sigmoid_grad.shapemape(
my_loss_sigmoid_grad,
loss_sigmoid_grad
)loss_tanh_grad = jacobian(lambda z: loss(tanh(z)))(z)
loss_tanh_grad.shapedelta_tanh = jacobian(loss)(tanh_pred)
delta_tanh.shape∂ L ∂ z p q ( k ) = ∑ i = 0 m ∑ j = 0 n o ∂ L ∂ a i j ( k ) ∂ a i j ( k ) ∂ z p q ( k ) \frac{\partial L}{\partial z^{(k)}_{pq}} =
\sum_{i=0}^{m} \sum_{j=0}^{n_{o}}
\frac{\partial L}{\partial a_{ij}^{(k)}}
\frac{\partial a_{ij}^{(k)}}{\partial z_{pq}^{(k)}} ∂ z pq ( k ) ∂ L = i = 0 ∑ m j = 0 ∑ n o ∂ a ij ( k ) ∂ L ∂ z pq ( k ) ∂ a ij ( k ) For the case i = p i=p i = p j = q j=q j = q
∂ a p q ( k ) ∂ z p q ( k ) = 1 − ( a p q ( k ) ) 2 \frac{\partial a_{pq}^{(k)}}
{\partial z_{pq}^{(k)}} =
1 - (a_{pq}^{(k)})^{2} ∂ z pq ( k ) ∂ a pq ( k ) = 1 − ( a pq ( k ) ) 2 For the case i ≠ p i \neq p i = p j ≠ q j \neq q j = q
∂ a i j ( k ) ∂ z p q ( k ) = 0 \frac{\partial a_{ij}^{(k)}}
{\partial z_{pq}^{(k)}} = 0 ∂ z pq ( k ) ∂ a ij ( k ) = 0 ∂ L ∂ z p q ( k ) = ∂ L ∂ a p q ( k ) ∂ a p q ( k ) ∂ z p q ( k ) = δ p q ( 1 − ( a p q ( k ) ) 2 ) \begin{align*}
\frac{\partial L}{\partial z^{(k)}_{pq}} &=
\frac{\partial L}{\partial a_{pq}^{(k)}}
\frac{\partial a_{pq}^{(k)}}{\partial z_{pq}^{(k)}} \\
&= \delta_{pq} \left(
1 - (a_{pq}^{(k)})^{2}
\right)
\end{align*} ∂ z pq ( k ) ∂ L = ∂ a pq ( k ) ∂ L ∂ z pq ( k ) ∂ a pq ( k ) = δ pq ( 1 − ( a pq ( k ) ) 2 ) for all p = m p = m p = m q = n k q = n_{k} q = n k
∂ L ∂ Z ( k ) = ∂ L ∂ A ( k ) ⊙ ∂ A ( k ) ∂ Z ( k ) = Δ ⊙ ( 1 − ( A ( k ) ) 2 ) \begin{align*}
\frac{\partial L}{\partial \mathbf{Z}^{(k)}} &=
\frac{\partial L}{\partial \mathbf{A}^{(k)}}
\odot
\frac{\partial \mathbf{A}^{(k)}}
{\partial \mathbf{Z}^{(k)}} \\ &=
\mathbf{\Delta} \odot
\left(
\mathbf{1} -
\left(
\mathbf{A}^{(k)}
\right)^{2}
\right)
\end{align*} ∂ Z ( k ) ∂ L = ∂ A ( k ) ∂ L ⊙ ∂ Z ( k ) ∂ A ( k ) = Δ ⊙ ( 1 − ( A ( k ) ) 2 ) def loss_tanh_der(delta: np.ndarray, tanh_out: np.ndarray) -> np.ndarray:
return np.multiply(delta, (1 - tanh_out ** 2))
my_loss_tanh_grad = loss_tanh_der(delta_tanh, tanh_pred)
my_loss_tanh_grad.shapemape(
my_loss_tanh_grad,
loss_tanh_grad
)In this section we will only use the ReLU function because we
don’t want to repeat the same code for each activation function,
and Sigmoid and Tanh have vanishing gradients.
∂ L ∂ Z ( k ) = Δ {\color{Cyan} {\frac{\partial L}
{\partial \mathbf{Z}^{(k)}}}} =
{\color{Cyan} {\mathbf{\Delta}}} ∂ Z ( k ) ∂ L = Δ bias_relu_grad = jacobian(lambda b: loss(relu(weighted_sum(X, weight, b))))(bias)
bias_relu_grad.shape∂ L ∂ b ( k ) = 1 Δ \frac{\partial L}{\partial \mathbf{b}^{(k)}} =
\mathbf{1 \Delta} ∂ b ( k ) ∂ L = 1Δ where 1 ∈ R m \mathbf{1} \in \mathbb{R}^{m} 1 ∈ R m
my_bias_relu_grad = np.sum(my_loss_relu_grad, axis=0)
my_bias_relu_grad.shapemape(
my_bias_relu_grad,
bias_relu_grad
)weight_relu_grad = jacobian(lambda w: loss(relu(weighted_sum(X, w, bias))))(weight)
weight_relu_grad.shape∂ L ∂ W ( k ) = ( A ( k − 1 ) ) ⊤ Δ \frac{\partial L}{\partial \mathbf{W}^{(k)}} =
(\mathbf{A}^{(k-1)})^{\top}
\mathbf{\Delta} ∂ W ( k ) ∂ L = ( A ( k − 1 ) ) ⊤ Δ where A ( k − 1 ) ∈ R m × n k − 1 \mathbf{A}^{(k-1)} \in \mathbb{R}^{m \times n_{k-1}} A ( k − 1 ) ∈ R m × n k − 1
my_weight_relu_grad = X.T @ my_loss_relu_grad
my_weight_relu_grad.shapemape(
my_weight_relu_grad,
weight_relu_grad
)input_relu_grad = jacobian(lambda x: loss(relu(weighted_sum(x, weight, bias))))(X)
input_relu_grad.shape∂ L ∂ a p q ( k − 1 ) = ∑ i = 1 m ∑ j = 1 n o ∂ L ∂ z i j ( k ) ∂ z i j ( k ) ∂ a p q ( k − 1 ) \frac{\partial L}{\partial a_{pq}^{(k-1)}} =
\sum_{i=1}^{m} \sum_{j=1}^{n_{o}}
\frac{\partial L}{\partial z_{ij}^{(k)}}
\frac{\partial z_{ij}^{(k)}}{\partial a_{pq}^{(k-1)}} ∂ a pq ( k − 1 ) ∂ L = i = 1 ∑ m j = 1 ∑ n o ∂ z ij ( k ) ∂ L ∂ a pq ( k − 1 ) ∂ z ij ( k ) ∂ z i j ( k ) ∂ a p q ( k − 1 ) = { w q j ( k ) if i = p 0 if i ≠ q \frac{\partial z_{ij}^{(k)}}{\partial a_{pq}^{(k-1)}} =
\begin{cases}
w_{qj}^{(k)} & \text{if } i=p \\
0 & \text{if } i \neq q
\end{cases} ∂ a pq ( k − 1 ) ∂ z ij ( k ) = { w q j ( k ) 0 if i = p if i = q ∂ L ∂ a p q ( k − 1 ) = ∑ j = 1 n o ∂ L ∂ z p j ( k ) ∂ z p j ( k ) ∂ a p q ( k − 1 ) = δ p , : ( w q , : ( k ) ) ⊤ \begin{align*}
\frac{\partial L}{\partial a_{pq}^{(k-1)}} &=
\sum_{j=1}^{n_{o}}
\frac{\partial L}{\partial z_{pj}^{(k)}}
\frac{\partial z_{pj}^{(k)}}{\partial a_{pq}^{(k-1)}} \\
&= \delta_{p,:} \left(
w_{q,:}^{(k)}
\right)^{\top}
\end{align*} ∂ a pq ( k − 1 ) ∂ L = j = 1 ∑ n o ∂ z p j ( k ) ∂ L ∂ a pq ( k − 1 ) ∂ z p j ( k ) = δ p , : ( w q , : ( k ) ) ⊤ for all p = 1 , … , m p=1, \ldots, m p = 1 , … , m q = 1 , … , n k − 1 q = 1, \ldots, n_{k-1} q = 1 , … , n k − 1
∂ L ∂ A ( k − 1 ) = Δ ( W ( k ) ) ⊤ \frac{\partial L}{\partial \mathbf{A}^{(k-1)}} =
\mathbf{\Delta} \left(
\mathbf{W}^{(k)}
\right)^{\top} ∂ A ( k − 1 ) ∂ L = Δ ( W ( k ) ) ⊤ my_input_relu_grad = my_loss_relu_grad @ weight.T
my_input_relu_grad.shapemape(
my_input_relu_grad,
input_relu_grad
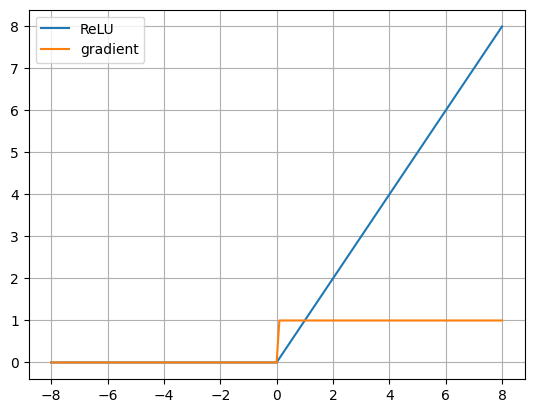
)The leakage gradient problem is a phenomenon that occurs during training.
It occurs when the gradients used to update the network are very small,
making it difficult for the network to efficiently update its weights.
This is a numerical stability problem.
from matplotlib import pyplot as plt
x = np.arange(-8.0, 8.1, 0.1)
x.shaperelu_out = relu(x)
relu_der = loss_relu_der(ones, relu_out)
plt.plot(x, relu_out, label='ReLU')
plt.plot(x, relu_der, label='gradient')
plt.grid(True)
plt.legend()
plt.show()soft_out = sigmoid(x)
soft_der = loss_sigmoid_der(ones, soft_out)
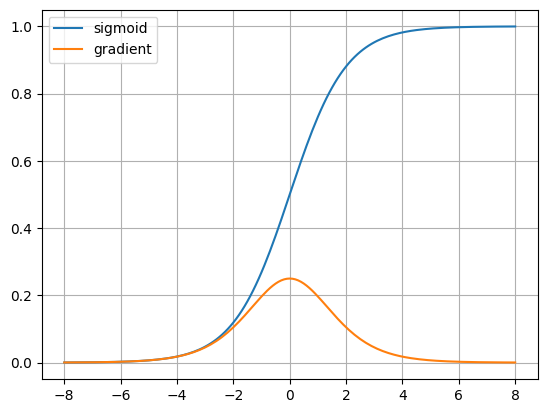
plt.plot(x, soft_out, label='sigmoid')
plt.plot(x, soft_der, label='gradient')
plt.grid(True)
plt.legend()
plt.show()tanh_out = tanh(x)
tanh_der = loss_tanh_der(ones, tanh_out)
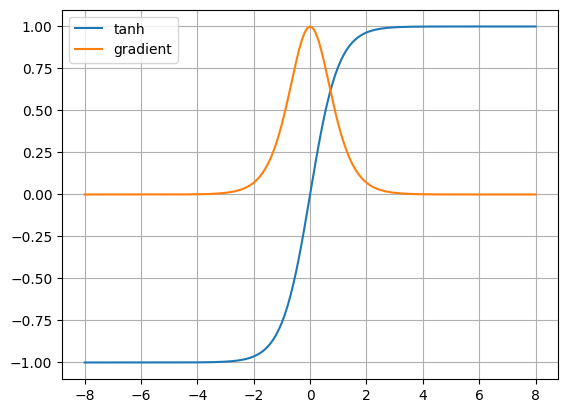
plt.plot(x, tanh_out, label='tanh')
plt.plot(x, tanh_der, label='gradient')
plt.grid(True)
plt.legend()
plt.show()We can observe that the sigmoid and tanh gradients tend to be 0
when the inputs are at the edges.
ReLU is the most numerically stable of these functions.
d Sigmoid d z = exp ( − z ) ( 1 + exp ( − z ) ) 2 = 1 1 + exp ( − z ) ( exp ( − z ) 1 + exp ( − z ) ) = 1 1 + exp ( − z ) ( 1 + exp ( − z ) 1 + exp ( − z ) − 1 1 + exp ( − z ) ) = 1 1 + exp ( − z ) ( 1 − 1 1 + exp ( − z ) ) = Sigmoid ( z ) ( 1 − Sigmoid ( z ) ) \begin{align*}
\frac{\mathrm{d} \text{Sigmoid}}{\mathrm{d} z}
&= \frac{\exp(-z)}{\left(1 + \exp(-z) \right)^{2}} \\
&= \frac{1}{1 + \exp(-z)} \left(
\frac{\exp(-z)}{1 + \exp(-z)}
\right) \\
&= \frac{1}{1 + \exp(-z)} \left(
\frac{1 + \exp(-z)}{1 + \exp(-z)} -
\frac{1}{1 + \exp(-z)}
\right) \\
&= \frac{1}{1 + \exp(-z)} \left(
1 - \frac{1}{1 + \exp(-z)}
\right) \\
&= \text{Sigmoid}(z) \left(1 - \text{Sigmoid}(z) \right)
\end{align*} d z d Sigmoid = ( 1 + exp ( − z ) ) 2 exp ( − z ) = 1 + exp ( − z ) 1 ( 1 + exp ( − z ) exp ( − z ) ) = 1 + exp ( − z ) 1 ( 1 + exp ( − z ) 1 + exp ( − z ) − 1 + exp ( − z ) 1 ) = 1 + exp ( − z ) 1 ( 1 − 1 + exp ( − z ) 1 ) = Sigmoid ( z ) ( 1 − Sigmoid ( z ) )