3.1 - MLP - Inside Deep Learning

The first advance we will make towards deep learning will be the multilayer perceptron (MLP). It consists of interconnecting several dense layers and superimposing them to obtain a deep neural network (DNN).

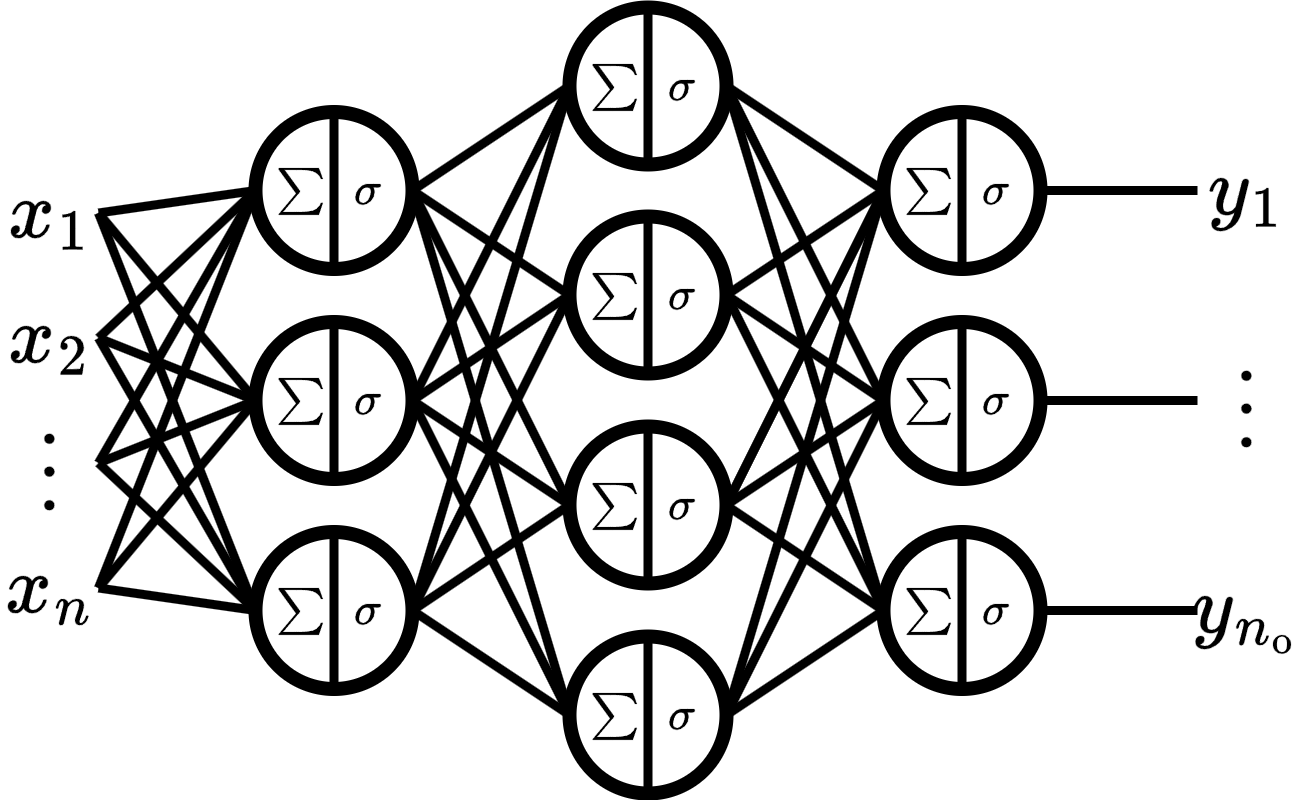
Purpose of this Notebook:

The purposes of this notebook are:

Create a dataset for linear regression task
Create our own Layer classes from scratch
- Dense
- Activation functions
Create our own MLP class from scratch
Calculate the backpropagation from scratch
Train our MLP
Compare our MLP to the one prebuilt by PyTorch

import torch
from torch import nn

from platform import python_version
python_version(), torch.__version__

('3.12.12', '2.9.0+cu128')

device = 'cpu'
if torch.cuda.is_available():
    device = 'cuda'
device

'cpu'

torch.set_default_dtype(torch.float64)

def add_to_class(Class):  
    """Register functions as methods in created class."""
    def wrapper(obj):
        setattr(Class, obj.__name__, obj)
    return wrapper

Dataset¶

create dataset¶

\mathbf{X} \in \mathbb{R}^{m \times n} \\ \mathbf{Y} \in \mathbb{R}^{m \times n_{o}}

(1)

from sklearn.datasets import make_regression
import random

M: int = 10_100 # number of samples
N: int = 6 # number of input features
NO: int = 3 # number of output features

X, Y = make_regression(
    n_samples=M, 
    n_features=N, 
    n_targets=NO, 
    n_informative=N - 1,
    bias=random.random(),
    noise=1
)

print(X.shape)
print(Y.shape)

(10100, 6)
(10100, 3)

split dataset into train and valid¶

X_train = torch.tensor(X[:1000], device=device)
X_valid = torch.tensor(X[1000:], device=device)
X_train.shape, X_valid.shape

(torch.Size([1000, 6]), torch.Size([9100, 6]))

Y_train = torch.tensor(Y[:1000], device=device)
Y_valid = torch.tensor(Y[1000:], device=device)
Y_train.shape, Y_valid.shape

(torch.Size([1000, 3]), torch.Size([9100, 3]))

delete raw dataset¶

del X
del Y

Model and layers¶

class Layer:
    is_trainable: bool = False
    pass


class Activation:
    pass


class Losses:
    pass

initialization¶

scratch model¶

The model as such will be the container of all our layers.

class Model:
    def __init__(self, layers: list[Layer], loss_f: Losses = None):
        self.layers = layers[1:] # do not save the input layer
        self.loss_f = MSE() if loss_f is None else loss_f

        # initialize all parameters
        out = layers[0].construct()
        for layer in self.layers:
            out = layer.construct(out)

    def copy_parameters(self, parameters) -> None:
        params = list(parameters())
        for layer in self.layers:
            if layer.is_trainable:
                layer.set_params(params.pop(0), params.pop(0))

layers¶

dense¶

dense or full conect layer.

\begin{align*} \mathbf{W}^{(k)} &\in \mathbb{R}^{n_{k-1} \times n_{k}} \\ \mathbf{b}^{(k)} &\in \mathbb{R}^{n_{k}} \end{align*}

(2)

for all $k = 1, \ldots, l$ . Where $l$ is the number of layers.

class Dense(Layer):
    def __init__(self, units: int, act_f: Activation = None):
        self.units = units
        self.act_f = act_f if act_f is not None else Linear()
        self.is_trainable = True

    def set_params(self, w: torch.Tensor, b: torch.Tensor) -> None:
        self.w.copy_(w.T.detach().clone())
        self.b.copy_(b.detach().clone())

    def construct(self, x: torch.Tensor) -> torch.Tensor:
        """
        Initialize the parameters.
        self.w := tensor (n_features, units).
        self.b := tensor (units).
        
        Args:
            x: input tensor of shape (m_samples, n_features).
        
        Return:
            z: out tensor of shape (m_samples, units).
        """
        n_features = x.shape[-1]
        self.w = torch.randn(n_features, self.units, device=device)
        self.b = torch.randn(self.units, device=device)
        return self.forward(x)

activation functions¶

For any activation function

\mathbf{A}^{(k)} : \mathbb{R}^{m \times n_{k}} \rightarrow \mathbb{R}^{m \times n_{k}}

(3)

for all $k = 1, \ldots, l$ .

class Linear(Activation):
    pass


class RelU(Activation):
    pass


class Sigmoid(Activation):
    pass


class Tanh(Activation):
    pass


class Softmax(Activation):
    pass

forward propagation¶

\begin{array}{l} \textbf{Algorithm 1: Forward propagation} \\ \mathbf{A}^{(0)} := \mathbf{X} \\ \textbf{for } k = 1 \text{ to } l \textbf{ do}\\ \quad \mathbf{Z}^{(k)} = \mathbf{A}^{(k-1)} \mathbf{W}^{(k)} + \mathbf{b}^{(k)} \\ \quad \mathbf{A}^{(k)} = f(\mathbf{Z}^{(k)}) \\ \textbf{end for} \end{array}

(4)

model¶

@add_to_class(Model)
def predict(self, x: torch.Tensor) -> torch.Tensor:
    """
    Forward propagation.
    
    Args:
        x: tensor of shape (m_samples, n_input_features).
        
    Return:
        y_pred: tensor of shape (m_samples, n_out_features).
    """
    out = x
    for layer in self.layers:
        out = layer.forward(out)
    return out

@add_to_class(Model)
def __forward__(self, x: torch.Tensor) -> torch.Tensor:
    out = x
    for layer in self.layers:
        out = layer.__forward__(out)
    return out

layers¶

dense¶

Weighted sum

\mathbf{Z}^{(k)}(\mathbf{A}^{(k-1)}) = \mathbf{A}^{(k-1)} \mathbf{W}^{(k)} + \mathbf{b}^{(k)} \\ \mathbf{Z}^{(k)} : \mathbb{R}^{m \times n_{k-1}} \rightarrow \mathbb{R}^{m \times n_{k}}

(5)

@add_to_class(Dense)
def forward(self, x: torch.Tensor) -> torch.Tensor:
    """
    Compute weighted sum Z = XW+b and activation function A = f(Z).
    
    Args:
        x: input tensor of shape (m_samples, n_features).
        
    Return:
        a: out tensor of shape (m_samples, units).
    """
    return self.act_f(torch.matmul(x, self.w) + self.b)

@add_to_class(Dense)
def __forward__(self, x: torch.Tensor) -> torch.Tensor:
    """Forward propagation for training step."""
    self.input = x.clone()
    self.a = self.forward(x)
    return self.a

activation functions¶

Linear¶

\text{Linear}^{(k)}(\mathbf{Z}^{(k)}) = \mathbf{Z}^{(k)}

(6)

@add_to_class(Linear)
def __call__(self, z: torch.Tensor) -> torch.Tensor:
    return z

ReLU¶

\text{ReLU}^{(k)}(\mathbf{Z^{(k)}}) = \max(\mathbf{Z^{(k)}}, 0)

(7)

@add_to_class(RelU)
def __call__(self, z: torch.Tensor) -> torch.Tensor:
    #return torch.relu(z)
    return torch.max(z, torch.zeros_like(z))

Sigmoid¶

\text{Sigmoid}^{(k)}(\mathbf{Z}^{(k)}) = \frac{1}{1 + \exp(-\mathbf{Z}^{(k)})}

(8)

@add_to_class(Sigmoid)
def __call__(self, z: torch.Tensor) -> torch.Tensor:
    #return torch.sigmoid(z)
    return 1 / (1 + torch.exp(-z))

Tanh¶

\tanh^{(k)}(\mathbf{Z}^{(k)}) = \frac{1 - \exp(-2 \mathbf{Z}^{(k)})} {1 + \exp(-2 \mathbf{Z}^{(k)})}

(9)

@add_to_class(Tanh)
def __call__(self, z: torch.Tensor) -> torch.Tensor:
    #return torch.tanh(z)
    exp = torch.exp(-2 * z)
    return (1 - exp) / (1 + exp)

Softmax¶

\text{Softmax}^{(k)} (\mathbf{Z}^{(k)}) = \begin{bmatrix} \sigma(\mathbf{z}_{1,:}) \\ \sigma(\mathbf{z}_{2,:}) \\ \vdots \\ \sigma(\mathbf{z}_{m,:}) \end{bmatrix}

(10)

@add_to_class(Softmax)
def __call__(self, z: torch.Tensor) -> torch.Tensor:
    exp = torch.exp(z - torch.max(z, dim=1, keepdims=True)[0])
    return exp / exp.sum(1, keepdims=True)

input layer¶

The purpose of this layer is simply to create a random dataset to initialize all the parameters of the layers. This way we do not have to manually specify the dimensions of each parameter.

class InputLayer(Layer):
    def __init__(self, n_input_features: int):
        self.m = 10
        self.n = n_input_features

    def construct(self) -> torch.Tensor:
        return torch.randn(self.m, self.n, device=device)

evaluation¶

loss function¶

\text{MSE}(\mathbf{A}^{(l)}) = \frac{1}{m n_{o}} \sum_{i=1}^{m} \sum_{j=1}^{n_{o}} \left( (a^{(l)}_{ij} - y_{ij})^2 \right)

(11)

where $\mathbf{A}^{(l)}$ is the activation of the last layer of the model and $n_{o}$ is the number of output features of the model.

class MSE(Losses):
    def loss(self, y_pred: torch.Tensor, y_true: torch.Tensor) -> float:
        return ((y_pred - y_true)**2).mean().item()

    def __call__(self, y_pred: torch.Tensor, y_true: torch.Tensor) -> float:
        return self.loss(y_pred, y_true)

model¶

@add_to_class(Model)
def evaluate(self, x: torch.Tensor, y: torch.Tensor) -> float:
    """
    Evaluate the model between input x and target y
    
    Args:
        x: tensor (m_samples, n_input_features).
        y: target tensor (m_samples, n_out_features).
        
    Return:
        loss: error between y_pred and target y.
    """
    y_pred = self.predict(x)
    return self.loss_f(y_pred, y)

backpropagation¶

We need to calculate the derivatives/gradients of each parameter in the model using backpropagation and update each parameter using gradient descent (gd).

The main idea of backpropagation is to calculate these derivatives

\frac{\partial L}{\partial \theta^{(l)}} = {\color{Lime} {\frac{\partial L} {\partial \mathbf{A}^{(l)}}}} {\color{Cyan} {\frac{\partial \mathbf{A}^{(l)}} {\partial \mathbf{Z}^{(l)}}}} {\color{Orange} {\frac{\partial \mathbf{Z}^{(l)}} {\partial \theta^{(l)}}}}

(12)

\frac{\partial L}{\partial \theta^{(l-1)}} = {\color{Lime} {\frac{\partial L} {\partial \mathbf{A}^{(l)}}}} {\color{Cyan} {\frac{\partial \mathbf{A}^{(l)}} {\partial \mathbf{Z}^{(l)}}}} {\color{Magenta} {\frac{\partial \mathbf{Z}^{(l)}} {\partial \mathbf{A}^{(l-1)}}}} {\color{Cyan} {\frac{\partial \mathbf{A}^{(l-1)}} {\partial \mathbf{Z}^{(l-1)}}}} {\color{Orange} {\frac{\partial \mathbf{Z}^{(l-1)}} {\partial \theta^{(l-1)}}}}

(13)

\frac{\partial L}{\partial \theta^{(k)}} = {\color{Lime} {\frac{\partial L} {\partial \mathbf{A}^{(l)}}}} {\color{Cyan} {\frac{\partial \mathbf{A}^{(l)}} {\partial \mathbf{Z}^{(l)}}}} {\color{Magenta} {\frac{\partial \mathbf{Z}^{(l)}} {\partial \mathbf{A}^{(l-1)}}}} \cdots {\color{Cyan} {\frac{\partial \mathbf{A}^{(k)}} {\partial \mathbf{Z}^{(k)}}}} {\color{Orange} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \theta^{(k)}}}}

(14)

where $\theta^{(k)} = (\mathbf{b}^{(k)}, \mathbf{W}^{(k)})$ .

It seems like there are many different derivatives. However, many of them are the same. We only need to know 4 derivatives

{\color{Lime} {\frac{\partial L} {\partial \mathbf{A}^{(l)}}}}, {\color{Cyan} {\frac{\partial \mathbf{A}^{(k)}} {\partial \mathbf{Z}^{(k)}}}}, {\color{Magenta} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \mathbf{A}^{(k-1)}}}}, {\color{Orange} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \theta^{(k)}}}}

(15)

With these 4 derivatives we can compute $\nabla_{\theta^{(k)}} L$ for all $k = l, \ldots, 1$ .

\begin{array}{l} \textbf{Algorithm 2: Backpropagation} \\ \mathbf{\Delta} := \nabla_{\mathbf{A}^{(l)}}L \\ \textbf{for } k = l, l-1, ..., 1 \textbf{ do}\\ \quad \mathbf{\Delta} := \mathbf{\Delta} \nabla_{\mathbf{Z}^{(k)}} \mathbf{A}^{(k)} \\ \quad \nabla_{\theta^{(k)}}L = \mathbf{\Delta} \nabla_{\theta^{(k)}} \mathbf{Z}^{(k)} \\ \quad \mathbf{\Delta} := \mathbf{\Delta} \nabla_{\mathbf{A}^{(k-1)}} \mathbf{Z}^{(k)} \\ \textbf{end for} \end{array}

(16)

model¶

@add_to_class(Model)    
def update(self, y_pred: torch.Tensor, y_true: torch.Tensor, lr: float) -> None:
    delta = self.loss_f.backward(y_pred, y_true)
    for layer in reversed(self.layers):
        delta = layer.backward(delta, lr)

loss function¶

@add_to_class(MSE)
def backward(self, y_pred: torch.Tensor, y_true: torch.Tensor) -> torch.Tensor:
    return 2 * (y_pred - y_true) / y_true.numel()

layers¶

activation functions¶

For more information about the derivatives of these activation functions, see gradients and activation functions.

Linear¶

@add_to_class(Linear)
def backward(self, delta, a):
    return delta

ReLU¶

@add_to_class(RelU)
def backward(self, delta, a):
    return delta * (1 * (a > 0))

Sigmoid¶

@add_to_class(Sigmoid)
def backward(self, delta, a):
    return delta * (a * (1 - a))

Tanh¶

@add_to_class(Tanh)
def backward(self, delta, a):
    return delta * (1 - a**2)

Softmax¶

@add_to_class(Softmax)
def backward(self, delta, a):
    return a * (delta - (delta * a).sum(axis=1, keepdims=True))

dense¶

respect to bias¶

\begin{align*} \frac{\partial L}{\partial \mathbf{b}^{(k)}} &= \frac{\partial L}{\partial \mathbf{Z}^{(k)}} {\color{Orange} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \mathbf{b}^{(k)}}}} \\ &= {\color{Orange} {\mathbf{1}}} \frac{\partial L}{\partial \mathbf{Z}^{(k)}} \end{align*}

(17)

where $\mathbf{1} \in \mathbb{R}^{m}$ .

respect to weight¶

\begin{align*} \frac{\partial L}{\partial \mathbf{W}^{(k)}} &= \frac{\partial L}{\partial \mathbf{Z}^{(k)}} {\color{Orange} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \mathbf{W}^{(k)}}}} \\ &= {\color{Orange} {\left( \mathbf{A}^{(k-1)} \right)^\top}} \frac{\partial L}{\partial \mathbf{Z}^{(k)}} \end{align*}

(18)

respect to input¶

\begin{align*} \frac{\partial L}{\partial \mathbf{A}^{(k-1)}} &= \frac{\partial L}{\partial \mathbf{Z}^{(k)}} {\color{Magenta} {\frac{\partial \mathbf{Z}^{(k)}} {\partial \mathbf{A}^{(k-1)}}}} \\ &= {\color{Magenta} {\left( \mathbf{W}^{(k)} \right)^\top}} \frac{\partial L}{\partial \mathbf{Z}^{(k)}} \end{align*}

(19)

gradient descent¶

\mathbf{W}^{(k)} := \mathbf{W}^{(k)} -\eta \nabla_{\mathbf{W}^{(k)}}L \\ \mathbf{b}^{(k)} := \mathbf{b}^{(k)} -\eta \nabla_{\mathbf{b}^{(k)}}L

(20)

@add_to_class(Dense)
def backward(self, delta, lr: float) -> torch.Tensor:
    # activation function derivative
    delta = self.act_f.backward(delta, self.a)
    # bias der and update
    self.b -= lr * torch.sum(delta, axis=0)
    # weight derivative (update weight after compute input der)
    w_der = torch.matmul(self.input.T, delta)
    # input derivative
    delta = torch.matmul(delta, self.w.T)
    # weight update
    self.w -= lr * w_der
    return delta

train¶

@add_to_class(Model)    
def fit(self, x_train: torch.Tensor, y_train: torch.Tensor, 
        epochs: int, lr: float, batch_size: int, 
        x_valid: torch.Tensor, y_valid: torch.Tensor):
    """
    Fit the model using gradient descent.

    Args:
        x_train: Input tensor of shape (n_samples, n_in_features).
        y_train: Target tensor one hot of shape (n_samples, n_out_features).
        epochs: Number of epochs to train.
        lr: learning rate).
        batch_size: Int number of batch.
        x_valid: Input tensor of shape (n_valid_samples, n_in_features).
        y_valid: Input tensor one hot of shape (n_valid_samples, n_out_features).
    """
    for epoch in range(epochs):
        loss_t = [] # train loss
        for batch in range(0, len(y_train), batch_size):
            end_batch = batch + batch_size

            y_pred = self.__forward__(x_train[batch:end_batch])
            loss_t.append(self.loss_f(y_pred, y_train[batch:end_batch]))

            self.update(y_pred, Y_train[batch:end_batch], lr)
            
        loss_t = sum(loss_t) / len(loss_t)
        loss_v = self.evaluate(x_valid, y_valid) # valid loss
        print('Epoch: {} - L: {:.4f} - L_v {:.4f}'.format(epoch, loss_t, loss_v))

Torch Sequential¶

class TorchSequential(nn.Module):
    def __init__(self, layers: list[nn.Module], loss_fn=None):
        super(TorchSequential, self).__init__()
        self.layers = nn.ModuleList(layers)
        for layer in self.layers:
            layer.to(device)
        self.loss_fn = loss_fn if loss_fn is not None else nn.MSELoss()
        self.eval()

    def forward(self, x):
        out = x.clone()
        for l in self.layers:
            out = l(out)
        return out

    def evaluate(self, x, y):
        self.eval()
        with torch.no_grad():
            y_pred = self(x)
            return self.loss_fn(y_pred, y).item()
        
    def fit(self, x: torch.Tensor, y: torch.Tensor, 
            epochs: int, lr: float, batch_size: int, 
            x_valid: torch.Tensor, y_valid: torch.Tensor):
        optimizer = torch.optim.SGD(self.parameters(), lr=lr, momentum=0.0)
        for epoch in range(epochs):
            loss_t = []
            for batch in range(0, len(y), batch_size):
                end_batch = batch + batch_size
                optimizer.zero_grad()

                y_pred = self(x[batch:end_batch])
                loss = self.loss_fn(y_pred, y[batch:end_batch])
                loss_t.append(loss.item())

                loss.backward()
                optimizer.step()
            loss_t = sum(loss_t) / len(loss_t)
            loss_v = self.evaluate(x_valid, y_valid)
            print('Epoch: {} - L: {:.4f} - L_v {:.4f}'.format(epoch, loss_t, loss_v))

torch_model = TorchSequential([
    nn.Linear(N, 32), nn.Tanh(),
    nn.Linear(32, 32), nn.Softmax(dim=1),
    nn.Linear(32, 32), nn.Sigmoid(),
    nn.Linear(32, 32), nn.ReLU(),
    nn.Linear(32, NO)
])

Scratch vs Sequential¶

scratch model¶

model = Model([
    InputLayer(N),
    Dense(32, Tanh()),
    Dense(32, Softmax()),
    Dense(32, Sigmoid()),
    Dense(32, RelU()),
    Dense(NO, Linear())
])

evals¶

import MAPE modified¶

# This cell imports torch_mape 
# if you are running this notebook locally 
# or from Google Colab.

import os
import sys

module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
    sys.path.append(module_path)

try:
    from tools.torch_metrics import torch_mape as mape
    print('mape imported locally.')
except ModuleNotFoundError:
    import subprocess

    repo_url = 'https://raw.githubusercontent.com/PilotLeoYan/inside-deep-learning/main/content/tools/torch_metrics.py'
    local_file = 'torch_metrics.py'
    
    subprocess.run(['wget', repo_url, '-O', local_file], check=True)
    try:
        from torch_metrics import torch_mape as mape # type: ignore
        print('mape imported from GitHub.')
    except Exception as e:
        print(e)

mape imported locally.

predict¶

mape(
    model.predict(X_valid),
    torch_model(X_valid)
)

15203.542226539805

copy parameters¶

model.copy_parameters(torch_model.parameters)

predict after copy parameters¶

mape(
    model.predict(X_valid),
    torch_model(X_valid)
)

4.061384031377773e-14

loss¶

mape(
    model.evaluate(X_valid, Y_valid),
    torch_model.evaluate(X_valid, Y_valid)
)

0.0

train¶

LR: float = 0.01
EPOCHS: int = 32
BATCH_SIZE: int = len(Y_train) // 3

torch_model.fit(
    X_train, Y_train.double(), 
    EPOCHS, LR, BATCH_SIZE, 
    X_valid, Y_valid.double()
)

Epoch: 0 - L: 16919.5256 - L_v 12733.7805
Epoch: 1 - L: 16836.0177 - L_v 12746.7505
Epoch: 2 - L: 16766.3862 - L_v 12733.5607
Epoch: 3 - L: 16680.7732 - L_v 12734.8370

Epoch: 4 - L: 16613.4161 - L_v 12737.8671

Epoch: 5 - L: 16549.5894 - L_v 12742.5114

Epoch: 6 - L: 16489.1086 - L_v 12748.6391
Epoch: 7 - L: 16431.7988 - L_v 12756.1273
Epoch: 8 - L: 16377.4943 - L_v 12764.8608
Epoch: 9 - L: 16326.0380 - L_v 12774.7315
Epoch: 10 - L: 16277.2809 - L_v 12785.6382

Epoch: 11 - L: 16231.0820 - L_v 12797.4859
Epoch: 12 - L: 16187.3075 - L_v 12810.1857
Epoch: 13 - L: 16145.8307 - L_v 12823.6545
Epoch: 14 - L: 16106.5312 - L_v 12837.8144
Epoch: 15 - L: 16069.2954 - L_v 12852.5926
Epoch: 16 - L: 16034.0152 - L_v 12867.9211
Epoch: 17 - L: 16000.5883 - L_v 12883.7364
Epoch: 18 - L: 15968.9178 - L_v 12899.9791
Epoch: 19 - L: 15938.9117 - L_v 12916.5941
Epoch: 20 - L: 15910.4830 - L_v 12933.5296
Epoch: 21 - L: 15883.5491 - L_v 12950.7376
Epoch: 22 - L: 15858.0317 - L_v 12968.1736
Epoch: 23 - L: 15833.8567 - L_v 12985.7958
Epoch: 24 - L: 15810.9539 - L_v 13003.5658
Epoch: 25 - L: 15789.2565 - L_v 13021.4476

Epoch: 26 - L: 15768.7015 - L_v 13039.4081
Epoch: 27 - L: 15749.2291 - L_v 13057.4164
Epoch: 28 - L: 15730.7824 - L_v 13075.4441
Epoch: 29 - L: 15713.3079 - L_v 13093.4649
Epoch: 30 - L: 15696.7544 - L_v 13111.4546
Epoch: 31 - L: 15681.0739 - L_v 13129.3907

model.fit(
    X_train, Y_train, 
    EPOCHS, LR, BATCH_SIZE, 
    X_valid, Y_valid
)

Epoch: 0 - L: 16919.5256 - L_v 12733.7805
Epoch: 1 - L: 16836.0177 - L_v 12746.7505
Epoch: 2 - L: 16766.3862 - L_v 12733.5607
Epoch: 3 - L: 16680.7732 - L_v 12734.8370
Epoch: 4 - L: 16613.4161 - L_v 12737.8671
Epoch: 5 - L: 16549.5894 - L_v 12742.5114

Epoch: 6 - L: 16489.1086 - L_v 12748.6391
Epoch: 7 - L: 16431.7988 - L_v 12756.1273
Epoch: 8 - L: 16377.4943 - L_v 12764.8608
Epoch: 9 - L: 16326.0380 - L_v 12774.7315
Epoch: 10 - L: 16277.2809 - L_v 12785.6382

Epoch: 11 - L: 16231.0820 - L_v 12797.4859
Epoch: 12 - L: 16187.3075 - L_v 12810.1857
Epoch: 13 - L: 16145.8307 - L_v 12823.6545
Epoch: 14 - L: 16106.5312 - L_v 12837.8144
Epoch: 15 - L: 16069.2954 - L_v 12852.5926
Epoch: 16 - L: 16034.0152 - L_v 12867.9211
Epoch: 17 - L: 16000.5883 - L_v 12883.7364

Epoch: 18 - L: 15968.9178 - L_v 12899.9791
Epoch: 19 - L: 15938.9117 - L_v 12916.5941
Epoch: 20 - L: 15910.4830 - L_v 12933.5296
Epoch: 21 - L: 15883.5491 - L_v 12950.7376
Epoch: 22 - L: 15858.0317 - L_v 12968.1736

Epoch: 23 - L: 15833.8567 - L_v 12985.7958
Epoch: 24 - L: 15810.9539 - L_v 13003.5658
Epoch: 25 - L: 15789.2565 - L_v 13021.4476
Epoch: 26 - L: 15768.7015 - L_v 13039.4081
Epoch: 27 - L: 15749.2291 - L_v 13057.4164
Epoch: 28 - L: 15730.7824 - L_v 13075.4441
Epoch: 29 - L: 15713.3079 - L_v 13093.4649

Epoch: 30 - L: 15696.7544 - L_v 13111.4546
Epoch: 31 - L: 15681.0739 - L_v 13129.3907

I know that both models are experiencing overfitting during training, but the goal of this notebook is not to create good predictors on synthetic data, but to understand their inner workings.

predict after train¶

mape(
    model.predict(X_valid),
    torch_model(X_valid)
)

4.666446909750489e-15

bias¶

filtered_layers = filter(
    lambda x: isinstance(x, nn.modules.linear.Linear), 
    torch_model.layers
)

for i, layer in enumerate(filtered_layers):
    print(f'scratch layer #{i} - torch layer #{i}')
    print(mape(model.layers[i].b, layer.bias))

scratch layer #0 - torch layer #0
4.8219658580436e-16
scratch layer #1 - torch layer #1
1.7582051394896728e-15
scratch layer #2 - torch layer #2
1.5460811307144968e-13
scratch layer #3 - torch layer #3
3.385663234501653e-14
scratch layer #4 - torch layer #4
4.6664469097504885e-15

weights¶

filtered_layers = filter(
    lambda x: isinstance(x, nn.modules.linear.Linear), 
    torch_model.layers
)

for i, layer in enumerate(filtered_layers):
    print(f'scratch layer #{i} - torch layer #{i}')
    print(mape(model.layers[i].w, layer.weight.T))

scratch layer #0 - torch layer #0
3.9396050401881644e-16
scratch layer #1 - torch layer #1
1.0474882746936395e-15
scratch layer #2 - torch layer #2
2.00276143830812e-15
scratch layer #3 - torch layer #3
4.343440088734276e-14
scratch layer #4 - torch layer #4
2.694056001041772e-14