1.1 - Simple Linear Regression - Inside Deep Learning

If we want to start with a topic before getting into deep learning, the perceptron is a good place to start, as it is the basic unit with which artificial neural networks (ANNs) are built. We can then use multiple perceptrons in parallel to form a dense layer. By using multiple dense layers, we can build a deep neural network (DNN).

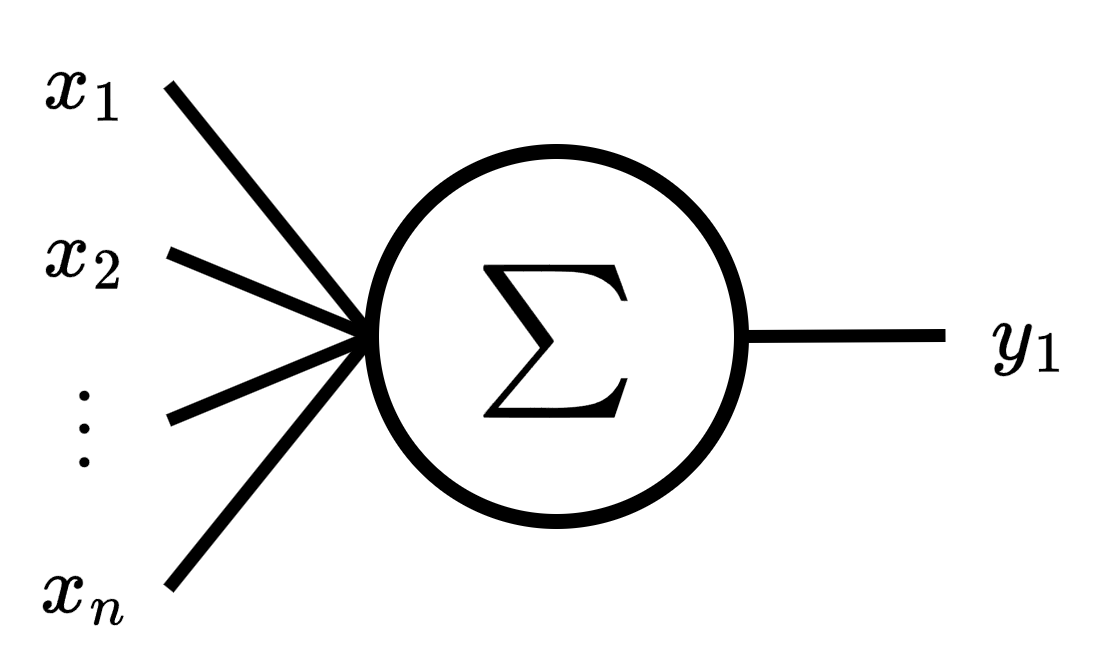
Our first topic is to train a perceptron for the simple linear regression task. We refer to “simple” as predicting a single output from multiple inputs.

\mathbb{R}^{n} \rightarrow \mathbb{R}

(1)

Purpose of this Notebook:

The purposes of this notebook are:

Create a dataset for linear regression task
Create our own Perceptron class from scratch
Calculate the gradient descent from scratch
Train our Perceptron
Compare our Perceptron to the one prebuilt by PyTorch

import torch
from torch import nn

from platform import python_version
python_version(), torch.__version__

('3.12.12', '2.9.0+cu128')

device = 'cpu'
if torch.cuda.is_available():
    device = 'cuda'
device

'cpu'

torch.set_default_dtype(torch.float64)

def add_to_class(Class):  
    """Register functions as methods in created class."""
    def wrapper(obj): setattr(Class, obj.__name__, obj)
    return wrapper

Dataset¶

create dataset¶

For our supervised task, we need two set $\mathbf{X}$ and $\mathbf{y}$ , where $\mathbf{X}$ is called input data and $\mathbf{y}$ is called target data. In this case, $\mathbf{X}$ and $\mathbf{y}$ are a matrix and a vector respectively.

\begin{align*} \mathbf{X} &\in \mathbb{R}^{m \times n} \\ \mathbf{y} &\in \mathbb{R}^{m} \end{align*}

(2)

where $m$ is the number of samples and $n$ is the number of features.

\mathbf{X} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{mn} \end{bmatrix}

(3)

\mathbf{y} = \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{bmatrix}

(4)

from sklearn.datasets import make_regression
import random

M: int = 10_100 # number of samples
N: int = 4 # number of features

X, Y = make_regression(
    n_samples=M, 
    n_features=N, 
    n_targets=1,
    n_informative=N - 1,
    bias=random.random(), # random true bias
    noise=1
)

print(X.shape)
print(Y.shape)

(10100, 4)
(10100,)

split dataset¶

X_train = torch.tensor(X[:100], device=device)
Y_train = torch.tensor(Y[:100], device=device)
X_train.shape, Y_train.shape

(torch.Size([100, 4]), torch.Size([100]))

X_valid = torch.tensor(X[100:], device=device)
Y_valid = torch.tensor(Y[100:], device=device)
X_valid.shape, Y_valid.shape

(torch.Size([10000, 4]), torch.Size([10000]))

delete raw dataset¶

del X
del Y

Scratch model¶

weight and bias¶

Trainable parameters

\begin{align*} \mathbf{w} &\in \mathbb{R}^{n} \\ b &\in \mathbb{R} \end{align*}

(5)

where $\mathbf{w}$ is called weight and $b$ is called bias.

\mathbf{w} = \begin{bmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{n} \end{bmatrix}

(6)

class SimpleLinearRegression:
    def __init__(self, n_features: int):
        self.w = torch.randn(n_features, device=device)
        self.b = torch.randn(1, device=device)

    def copy_params(self, torch_layer: nn.modules.linear.Linear):
        """
        Copy the parameters from a module.linear to this model.

        Args:
            torch_layer: Pytorch module from which to copy the parameters.
        """
        self.b.copy_(torch_layer.bias.detach().clone())
        self.w.copy_(torch_layer.weight[0,:].detach().clone())

weighted sum¶

\begin{align*} \mathbf{\hat{y}}(\mathbf{X}) = \mathbf{X}\mathbf{w} + b \\ \mathbf{\hat{y}} : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m} \end{align*}

(7)

where $\mathbf{\hat{y}}$ is called predicted output data.

\begin{align*} \mathbf{\hat{y}} &= \mathbf{X} \mathbf{w} + b \\ &= \begin{bmatrix} \mathbf{x}_{1}^\top \\ \mathbf{x}_{2}^\top \\ \vdots \\ \mathbf{x}_{m}^\top \\ \end{bmatrix} \mathbf{w} + b \\ &= \begin{bmatrix} \mathbf{x}_{1}^\top \mathbf{w} + b \\ \mathbf{x}_{2}^\top \mathbf{w} + b \\ \vdots \\ \mathbf{x}_{m}^\top \mathbf{w} + b \\ \end{bmatrix} \end{align*}

(8)

where

\mathbf{x}_{i}^\top = \begin{bmatrix} x_{i1} & x_{i2} & \cdots & x_{in} \end{bmatrix}

(9)

@add_to_class(SimpleLinearRegression)
def predict(self, x: torch.Tensor) -> torch.Tensor:
    """
    Predict the output for input x.

    Args:
        x: Input tensor of shape (n_samples, n_features).

    Returns:
        y_pred: Predicted output tensor of shape (n_samples,).
    """
    return torch.matmul(x, self.w) + self.b

MSE¶

We need a loss function. We will use Mean Squared Error (MSE)

\begin{align*} L(\mathbf{\hat{y}}) &= \frac{1}{m} \sum_{i=1}^{m}( \hat{y}_i - y_i)^{2} \\ L &: \mathbb{R}^{m} \rightarrow \mathbb{R} \end{align*}

(10)

Vectorized form

\begin{align*} L(\mathbf{\hat{y}}) &= \frac{1}{m} \left\| \mathbf{e} \right\|_{2}^2 \\ \mathbf{e} &:= \mathbf{\hat{y}} - \mathbf{y} \end{align*}

(11)

@add_to_class(SimpleLinearRegression)
def mse_loss(self, y_true: torch.Tensor, y_pred: torch.Tensor):
    """
    MSE loss function between target y_true and y_pred.

    Args:
        y_true: Target tensor of shape (n_samples,).
        y_pred: Predicted tensor of shape (n_samples,).

    Returns:
        loss: MSE loss between predictions and true values.
    """
    return ((y_pred - y_true)**2).mean().item()

@add_to_class(SimpleLinearRegression)
def evaluate(self, x: torch.Tensor, y_true: torch.Tensor):
    """
    Evaluate the model on input x and target y_true using MSE.

    Args:
        x: Input tensor of shape (n_samples, n_features).
        y_true: Target tensor of shape (n_samples,).

    Returns:
        loss: MSE loss between predictions and true values.
    """
    y_pred = self.predict(x)
    return self.mse_loss(y_true, y_pred)

computing gradients¶

Gradient descent is

\frac{\partial L}{\partial b} = \frac{\partial L}{\partial \mathbf{\hat{y}}} \frac{\partial \mathbf{\hat{y}}}{\partial b}

(12)

\frac{\partial L}{\partial \mathbf{w}} = \frac{\partial L}{\partial \mathbf{\hat{y}}} \frac{\partial \mathbf{\hat{y}}}{\partial \mathbf{w}}

(13)

where their shapes are

\frac{\partial L}{\partial \mathbf{w}} \in \mathbb{R}^{n}, \frac{\partial L}{\partial b} \in \mathbb{R}, \frac{\partial L}{\partial \mathbf{\hat{y}}} \in \mathbb{R}^{m}, \frac{\partial \mathbf{\hat{y}}}{\partial \mathbf{w}} \in \mathbb{R}^{m \times n}, \frac{\partial \mathbf{\hat{y}}}{\partial b} \in \mathbb{R}^{m}

(14)

MSE derivative¶

\frac{\partial L}{\partial \mathbf{\hat{y}}} = \begin{bmatrix} \frac{\partial L}{\partial \hat{y}_{1}} & \frac{\partial L}{\partial \hat{y}_{2}} & \cdots & \frac{\partial L}{\partial \hat{y}_{m}} \end{bmatrix}^\top

(15)

where

\begin{align*} \frac{\partial L}{\partial \hat{y}_{p}} &= \frac{\partial}{\partial \hat{y}_{p}} \left( \frac{1}{m} \sum_{i=1}^{m}( \hat{y}_i - y_i)^{2} \right) \\ &= \frac{2}{m} (\hat{y}_{p} - y_{p}) \end{align*}

(16)

for all $p = 1, \ldots, m$ .

therefore

\frac{\partial L}{\partial \mathbf{\hat{y}}} = \frac{2}{m} \left( \mathbf{\hat{y}} - \mathbf{y} \right)

(17)

weighted sum derivative¶

respect to bias¶

\frac{\partial \mathbf{\hat{y}}}{\partial b} = \begin{bmatrix} \frac{\partial \hat{y}_{1}}{\partial b} & \frac{\partial \hat{y}_{2}}{\partial b} & \cdots & \frac{\partial \hat{y}_{m}}{\partial b} \end{bmatrix}^\top

(18)

where

\begin{align*} \frac{\partial \hat{y}_{p}}{\partial b} &= \frac{\partial}{\partial b} \left( \mathbf{x}_{p}^\top \mathbf{w} + b \right) \\ &= 1 \end{align*}

(19)

for all $p = 1, \ldots, m$ .

therefore

\frac{\partial \mathbf{\hat{y}}}{\partial b} = \mathbf{1} \in \mathbb{R}^{m}

(20)

respect to weight¶

\frac{\partial \mathbf{\hat{y}}}{\partial \mathbf{w}} = \begin{bmatrix} \frac{\partial \hat{y}_{1}}{\partial w_{1}} & \frac{\partial \hat{y}_{1}}{\partial w_{2}} & \cdots & \frac{\partial \hat{y}_{1}}{\partial w_{n}} \\ \frac{\partial \hat{y}_{2}}{\partial w_{1}} & \frac{\partial \hat{y}_{2}}{\partial w_{2}} & \cdots & \frac{\partial \hat{y}_{2}}{\partial w_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial \hat{y}_{m}}{\partial w_{1}} & \frac{\partial \hat{y}_{m}}{\partial w_{2}} & \cdots & \frac{\partial \hat{y}_{m}}{\partial w_{n}} \end{bmatrix}

(21)

where

\begin{align*} \frac{\partial \hat{y}_{p}}{\partial w_{q}} &= \frac{\partial}{\partial w_{q}} \left( \mathbf{x}_{p}^\top \mathbf{w} + b \right) \\ &= x_{pq} \end{align*}

(22)

for all $p = 1, \ldots, m$ and $q = 1, \ldots, n$ .

therefore

\frac{\partial \mathbf{\hat{y}}}{\partial \mathbf{w}} = \mathbf{X}

(23)

gradients¶

\begin{align*} \nabla_{b}L = \frac{\partial L}{\partial b} &= {\color{Cyan} {\frac{\partial L}{\partial \mathbf{\hat{y}}}}} {\color{Orange} {\frac{\partial \mathbf{\hat{y}}}{\partial b}}} \\ &= {\color{Cyan} {\frac{2}{m} \left(\mathbf{\hat{y}} - \mathbf{y} \right)}} {\color{Orange} {\mathbf{1}}} \end{align*}

(24)

\begin{align*} \nabla_{\mathbf{w}}L = \frac{\partial L}{\partial \mathbf{w}} &= {\color{Cyan} {\frac{\partial L}{\partial \mathbf{\hat{y}}}}} {\color{Magenta} {\frac{\partial \mathbf{\hat{y}}}{\partial \mathbf{w}}}} \\ &= {\color{Cyan} {\frac{2}{m} \left(\mathbf{\hat{y}} - \mathbf{y} \right)}} {\color{Magenta} {\mathbf{X}}} \end{align*}

(25)

parameters update¶

\begin{align*} \mathbf{w} := \mathbf{w} -\eta \nabla_{\mathbf{w}}L &= \mathbf{w} -\eta \left( \frac{2}{m} (\mathbf{\hat{y}} - \mathbf{y}) \mathbf{X} \right) \\ b := b -\eta \nabla_{b}L &= b -\eta \left( \frac{2}{m} (\mathbf{\hat{y}} - \mathbf{y}) \mathbf{1} \right) \end{align*}

(26)

where $\eta$ is called learning rate.

@add_to_class(SimpleLinearRegression)
def update(self, x: torch.Tensor, y_true: torch.Tensor, y_pred: torch.Tensor, lr: float):
    """
    Update the model parameters.

    Args:
       x: Input tensor of shape (n_samples, n_features).
       y_true: Target tensor of shape (n_samples,).
       y_pred: Predicted output tensor of shape (n_samples,).
       lr: Learning rate. 
    """
    delta = 2 * (y_pred - y_true) / len(y_true)
    self.b -= lr * delta.sum()
    self.w -= lr * torch.matmul(delta, x)

gradient descent¶

We have assumed that we will use the entire train dataset to update our parameters, but we can use only a fraction of the samples in our train dataset to update our parameters. There are mainly 3 ways to use Gradient descent (GD).

batch GD
stochastic GD (SGD)
mini-batch GD

batch GD¶

The batch GD uses all samples of train dataset to update our parameters:

\begin{array}{l} \textbf{Algorithm 1: batch Gradient Descent} \\ \textbf{for } t = 1 \text{ to } T \textbf{ do}\\ \quad \mathbf{\theta} \leftarrow \text{update}(\mathbf{X}, \mathbf{y}; \mathbf{\theta}) \\ \textbf{end for} \end{array}

(27)

where $T$ is the number of epochs.
Remark: $\mathbf{\theta}$ is an arbitrary parameter, for this model we have to update $\mathbf{w}$ and $b$ .

stochastic GD (SGD)¶

The SGD for each epoch, we update our parameters for each sample in our train dataset:

\begin{array}{l} \textbf{Algorithm 2: stochastic Gradient Descent (SGD)} \\ \textbf{for } t = 1 \text{ to } T \textbf{ do}\\ \quad \textbf{for } i = 1 \text{ to } m \textbf{ do} \\ \quad \quad \mathbf{\theta} \leftarrow \text{update}(\mathbf{X}_{i,:}, y_{i}; \mathbf{\theta}) \\ \textbf{end for} \end{array}

(28)

where $\mathbf{X}_{i,:}$ and $y_{i}$ are the $i$ -th input and $i$ -th output sample of the train dataset respectly.
Note: $\mathbf{X}_{i,:} \in \mathbb{R}^{1 \times n}$ and $y_{i} \in \mathbb{R}$ .

mini-batch GD¶

The mini-batch GD is intermediate between SGD and batch GD since a fraction of the dataset larger than SGD but smaller than batch GD is used to update our parameters per epoch:

\begin{array}{l} \textbf{Algorithm 3: mini-batch Gradient Descent} \\ \textbf{for } t = 1 \text{ to } T \textbf{ do} \\ \quad i \leftarrow 1 \\ \quad j \leftarrow \mathcal{B} \\ \quad \textbf{while } i < m \textbf{ do} \\ \quad \quad \mathbf{\theta} \leftarrow \text{update}(\mathbf{X}_{i:j,:}, \mathbf{y}_{i:j}; \mathbf{\theta}) \\ \quad \quad i \leftarrow i + \mathcal{B} \\ \quad \quad j \leftarrow j + \mathcal{B} \\ \textbf{end for} \end{array}

(29)

where $\mathcal{B}$ is the number of samples per minibatch and $\mathbf{X}_{i:j,:}$ and $\mathbf{y}_{i:j}$ are the $i$ -th to $j$ -th samples.
Note: If $\mathcal{B}=1$ , then mini-batch GD becomes SGD. And if $\mathcal{B}=m$ , then mini-batch GD becomes batch GD.

@add_to_class(SimpleLinearRegression)
def fit(self, x: torch.Tensor, y: torch.Tensor, 
        epochs: int, lr: float, batch_size: int, 
        x_valid: torch.Tensor, y_valid: torch.Tensor):
    """
    Fit the model using gradient descent.
    
    Args:
        x: Input tensor of shape (n_samples, n_features).
        y: Target tensor of shape (n_samples,).
        epochs: Number of epochs to fit.
        lr: learning rate.
        batch_size: Int number of batch.
        x_valid: Input tensor of shape (n_valid_samples, n_features).
        y_valid: Target tensor of shape (n_valid_samples,).
    """
    for epoch in range(epochs):
        loss = []
        for batch in range(0, len(y), batch_size):
            end_batch = batch + batch_size

            y_pred = self.predict(x[batch:end_batch])

            loss.append(self.mse_loss(
                y[batch:end_batch],
                y_pred
            ))

            self.update(
                x[batch:end_batch], 
                y[batch:end_batch], 
                y_pred, 
                lr
            )

        loss = round(sum(loss) / len(loss), 4)
        loss_v = round(self.evaluate(x_valid, y_valid), 4)
        print(f'epoch: {epoch} - MSE: {loss} - MSE_v: {loss_v}')

Scratch vs Torch.nn¶

Torch.nn model¶

class TorchLinearRegression(nn.Module):
    def __init__(self, n_features):
        super(TorchLinearRegression, self).__init__()
        self.layer = nn.Linear(n_features, 1, device=device)
        self.loss = nn.MSELoss()

    def forward(self, x):
        return self.layer(x)
    
    def evaluate(self, x, y):
        self.eval()
        with torch.no_grad():
            y_pred = self.forward(x)
            return self.loss(y_pred, y).item()
    
    def fit(self, x, y, epochs, lr, batch_size, x_valid, y_valid):
        optimizer = torch.optim.SGD(self.parameters(), lr=lr)
        for epoch in range(epochs):
            loss_t = [] # train loss
            for batch in range(0, len(y), batch_size):
                end_batch = batch + batch_size

                y_pred = self.forward(x[batch:end_batch])
                loss = self.loss(y_pred, y[batch:end_batch])
                loss_t.append(loss.item())

                optimizer.zero_grad()
                loss.backward()
                optimizer.step()

            loss_t = round(sum(loss_t) / len(loss_t), 4)
            loss_v = round(self.evaluate(x_valid, y_valid), 4)
            print(f'epoch: {epoch} - MSE: {loss_t} - MSE_v: {loss_v}')
        optimizer.zero_grad()

torch_model = TorchLinearRegression(N)

scratch model¶

model = SimpleLinearRegression(N)

evals¶

import MAPE modified¶

# This cell imports torch_mape 
# if you are running this notebook locally 
# or from Google Colab.

import os
import sys

module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
    sys.path.append(module_path)

try:
    from tools.torch_metrics import torch_mape as mape
    print('mape imported locally.')
except ModuleNotFoundError:
    import subprocess

    repo_url = 'https://raw.githubusercontent.com/PilotLeoYan/inside-deep-learning/main/content/tools/torch_metrics.py'
    local_file = 'torch_metrics.py'
    
    subprocess.run(['wget', repo_url, '-O', local_file], check=True)
    try:
        from torch_metrics import torch_mape as mape # type: ignore
        print('mape imported from GitHub.')
    except Exception as e:
        print(e)

mape imported locally.

predict¶

mape(
    model.predict(X_valid),
    torch_model.forward(X_valid).squeeze(-1)
)

3447.2241178621794

copy parameters¶

model.copy_params(torch_model.layer)

predict after copy parameters¶

mape(
    model.predict(X_valid),
    torch_model.forward(X_valid).squeeze(-1)
)

0.0

loss¶

mape(
    model.evaluate(X_valid, Y_valid),
    torch_model.evaluate(X_valid, Y_valid.unsqueeze(-1))
)

0.0

training¶

LR = 0.01 # learning rate
EPOCHS = 16 # number of epochs
BATCH = len(X_train) // 3 # number of minibatch

torch_model.fit(
    X_train, 
    Y_train.unsqueeze(-1),
    EPOCHS, LR, BATCH,
    X_valid,
    Y_valid.unsqueeze(-1)
)

epoch: 0 - MSE: 8327.4864 - MSE_v: 8157.4615
epoch: 1 - MSE: 7137.4902 - MSE_v: 7025.4753
epoch: 2 - MSE: 6120.8559 - MSE_v: 6054.2807
epoch: 3 - MSE: 5251.8738 - MSE_v: 5220.5685
epoch: 4 - MSE: 4508.7119 - MSE_v: 4504.4714
epoch: 5 - MSE: 3872.8212 - MSE_v: 3889.0472
epoch: 6 - MSE: 3328.4343 - MSE_v: 3359.8405
epoch: 7 - MSE: 2862.1411 - MSE_v: 2904.5115
epoch: 8 - MSE: 2462.5309 - MSE_v: 2512.5203
epoch: 9 - MSE: 2119.8892 - MSE_v: 2174.8604
epoch: 10 - MSE: 1825.9413 - MSE_v: 1883.831
epoch: 11 - MSE: 1573.6354 - MSE_v: 1632.8447
epoch: 12 - MSE: 1356.9592 - MSE_v: 1416.2634
epoch: 13 - MSE: 1170.7837 - MSE_v: 1229.2591
epoch: 14 - MSE: 1010.7313 - MSE_v: 1067.6952
epoch: 15 - MSE: 873.0641 - MSE_v: 928.0258

model.fit(
    X_train, Y_train,
    EPOCHS, LR, BATCH,
    X_valid, Y_valid
)

epoch: 0 - MSE: 8327.4864 - MSE_v: 8157.4615
epoch: 1 - MSE: 7137.4902 - MSE_v: 7025.4753
epoch: 2 - MSE: 6120.8559 - MSE_v: 6054.2807
epoch: 3 - MSE: 5251.8738 - MSE_v: 5220.5685
epoch: 4 - MSE: 4508.7119 - MSE_v: 4504.4714
epoch: 5 - MSE: 3872.8212 - MSE_v: 3889.0472
epoch: 6 - MSE: 3328.4343 - MSE_v: 3359.8405
epoch: 7 - MSE: 2862.1411 - MSE_v: 2904.5115
epoch: 8 - MSE: 2462.5309 - MSE_v: 2512.5203
epoch: 9 - MSE: 2119.8892 - MSE_v: 2174.8604
epoch: 10 - MSE: 1825.9413 - MSE_v: 1883.831
epoch: 11 - MSE: 1573.6354 - MSE_v: 1632.8447
epoch: 12 - MSE: 1356.9592 - MSE_v: 1416.2634
epoch: 13 - MSE: 1170.7837 - MSE_v: 1229.2591
epoch: 14 - MSE: 1010.7313 - MSE_v: 1067.6952
epoch: 15 - MSE: 873.0641 - MSE_v: 928.0258

predict after training¶

mape(
    model.predict(X_valid),
    torch_model.forward(X_valid).squeeze(-1)
)

5.088568285940422e-14

weight¶

mape(
    model.w.clone(),
    torch_model.layer.weight.detach().squeeze(0)
)

1.8137912640341185e-14

bias¶

mape(
    model.b.clone(),
    torch_model.layer.bias.detach()
)

0.0